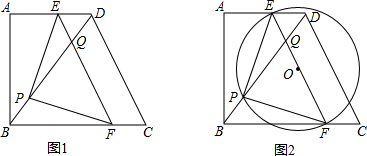题目内容
20. 在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合(如图),(1)求证:四边形BEDF是菱形;
在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合(如图),(1)求证:四边形BEDF是菱形;(2)求折痕EF的长.
分析 (1)EF与BD相交于点O,根据折叠的性质得到ED=EB,FD=FB,EF⊥BD,则∠EDB=∠EBD,由DC∥AB得∠EBD=∠CDB,则∠EDO=∠FDO,而DO⊥EF,可得△DEF为等腰三角形,得到DE=EB=BF=FD,于是可判断四边形DEBF为菱形;
(2)先利用勾股定理计算出BD=10,设BE=x,则DE=x,AE=8-x,在Rt△ABE中根据勾股定理得到62+(8-x)2=x2,可解得x=$\frac{25}{4}$,然后根据菱形的面积公式计算EF的长.
解答 解:(1)EF与BD相交于点O,如图
∵矩形ABCD纸片折叠,使点D与点B重合,
∴EF垂直平分BD,
∴ED=EB,FD=FB,EF⊥BD,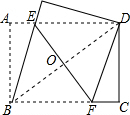
∴∠EDB=∠EBD,
∵DC∥AB,
∴∠ABD=∠CDB,
∴∠EDO=∠FDO,
而DO⊥EF,
∴△DEF为等腰三角形,
∴DF=DE,
∴DE=EB=BF=FD,
∴四边形DEBF为菱形;
(2)在Rt△ABD中,BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10,
设BE=x,则DE=x,AE=8-x,
在Rt△ABE中,AB2+AE2=DE2,即62+(8-x)2=x2,解得x=$\frac{25}{4}$,
即BE=$\frac{25}{4}$,
∵$\frac{1}{2}$S菱形DEBF=S三角形DEB
∴$\frac{1}{2}$×$\frac{1}{2}$EF•DB=$\frac{1}{2}$DE•AB,
∴$\frac{1}{2}$×EF×10=6×$\frac{25}{4}$,
∴EF=$\frac{15}{2}$.
点评 本题考查折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;对应点的连线段被折痕垂直平分.也考查了矩形的性质、菱形的判定方法以及勾股定理.

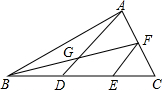 如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )
如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )| A. | 1:1 | B. | 3:2 | C. | 9:4 | D. | 4:3 |
 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )| A. | 2$\sqrt{10}$-2 | B. | 6 | C. | 2$\sqrt{13}$-2 | D. | 4 |
 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 5 | D. | 6 |
 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P在AC边上,点M、N在AB边上,(点M在点N的左侧),PM=PN,且∠MPN=∠A,连接CN.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P在AC边上,点M、N在AB边上,(点M在点N的左侧),PM=PN,且∠MPN=∠A,连接CN. 如图,是一个小正方形边长为1的8×8的网格,请你在网格中画出一个面积为6的
如图,是一个小正方形边长为1的8×8的网格,请你在网格中画出一个面积为6的