题目内容
现有边长为a的A类正方形卡片和边长为b的B类正方形卡片,及长为a,宽为b的C类长方形卡片各若干张,如果要拼成一个长为(a+2b)、宽为(2a+b)的大长方形,需要A类卡片 张,B类卡片 张,C类卡片 张.
考点:多项式乘多项式
专题:
分析:根据长方形的面积等于长乘以宽列式,再根据多项式的乘法法则计算,然后结合卡片的面积即可作出判断.
解答:解:长为a+2b,宽为2a+b的矩形面积为(a+2b)(2a+b)=2a2+5ab+2b2,
A图形面积为a2,B图形面积为b2,C图形面积为ab,
则可知需要A类卡片2张,B类卡片2张,C类卡片5张.
故本题答案为:2;2;5.
A图形面积为a2,B图形面积为b2,C图形面积为ab,
则可知需要A类卡片2张,B类卡片2张,C类卡片5张.
故本题答案为:2;2;5.
点评:此题的立意较新颖,主要考查多项式的乘法,熟练掌握运算法则是解题的关键.

练习册系列答案
相关题目
 若关于x的不等式3x-m<2的解集如图所示,则m的值为
若关于x的不等式3x-m<2的解集如图所示,则m的值为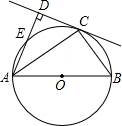 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.