题目内容
10.观察下列图案:
它们是按照一定规律排列的,依照此规律,第100个图案中共有三角形402个.
分析 观察图形得到第1个图案中有2×2+2×1=6个三角形;第2个图案中有2×3+2×2=10个三角形;第3个图案中有2×4+2×3=14个三角形;则第n个图案中有2×(n+1)+2×n个三角形,然后把n=100代入计算即可.
解答 解:∵第1个图案中有2×2+2×1=6个三角形;
第2个图案中有2×3+2×2=10个三角形;
第3个图案中有2×4+2×3=14个三角形;
…
∴第n个图案中有2×(n+1)+2×n个三角形,
∴第100个图案中有2×101+2×100=402个三角形.
故答案为:402.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1. 如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
 如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |
18.下列运算正确的是( )
| A. | a3+a=2a4 | B. | a6÷a-3=a3 | C. | a3•a3=2a3 | D. | (-2a2)3=-8a6 |
2.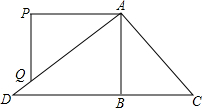 如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
 如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
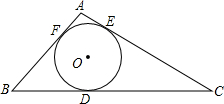 已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.
已知:如图,⊙O是△ABC的内切圆,分别切BC、AB、AC于点D、E、F,△ABC的周长为24cm,BC=10cm,则AE=2cm.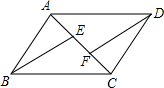 已知平行四边形ABCD中,BE∥DF,求证:AE=CF.
已知平行四边形ABCD中,BE∥DF,求证:AE=CF. 如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.
如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.