题目内容
抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.
(1)求这条抛物线的函数关系式;
(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.
(1)求这条抛物线的函数关系式;
(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.
考点:抛物线与x轴的交点,等腰三角形的判定
专题:
分析:(1)由抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),可得点A是抛物线的顶点,则可得x=
=1,则可求得a的值,继而求得这条抛物线的函数关系式;
(2)首先求得点B的坐标,然后分别从AB=AC,BA=BC,CA=CB去分析求解即可求得答案.
| 2 |
| 2a |
(2)首先求得点B的坐标,然后分别从AB=AC,BA=BC,CA=CB去分析求解即可求得答案.
解答:解:(1)∵抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),
∴点A是抛物线的顶点,
∴x=
=1,
∴a=-1,
∴这条抛物线的函数关系式为:y=-(x-1)2+4=-x2+2x+3;
(2)∵抛物线与x轴正半轴交于点B,
∴0=-(x-1)2+4,
解得:x=3或x=-1,
∴点B(3,0),
若点A、B与抛物线对称轴上的点C构成等腰三角形,有三种可能:
当AB=AC时,点C(1,4±2
);
当BA=BC时,点C(1,-4);
当CA=CB时,点C(1,
);
综上所述,点C的坐标为:(1,4+2
),(1,4-2
),(1,-4),(1,
).
∴点A是抛物线的顶点,
∴x=
| 2 |
| 2a |
∴a=-1,
∴这条抛物线的函数关系式为:y=-(x-1)2+4=-x2+2x+3;
(2)∵抛物线与x轴正半轴交于点B,
∴0=-(x-1)2+4,
解得:x=3或x=-1,
∴点B(3,0),
若点A、B与抛物线对称轴上的点C构成等腰三角形,有三种可能:
当AB=AC时,点C(1,4±2
| 5 |
当BA=BC时,点C(1,-4);
当CA=CB时,点C(1,
| 3 |
| 2 |
综上所述,点C的坐标为:(1,4+2
| 5 |
| 5 |
| 3 |
| 2 |
点评:此题考查了二次函数的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.
如图所示,有一等腰三角形钢板,其腰AB=40cm,底边BC为48cm,求这个钢板零件的面积.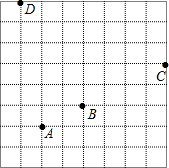 如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.