题目内容
 如图,现测量河宽AB(假设河的两岸平行),在点C测得∠ACB=30°,在点D测得∠ADB=45°.若CD=60m,则河宽AB为
如图,现测量河宽AB(假设河的两岸平行),在点C测得∠ACB=30°,在点D测得∠ADB=45°.若CD=60m,则河宽AB为考点:解直角三角形的应用
专题:
分析:先根据三角形外角的性质求出∠CAD的度数,判断出△ACD的形状,再由锐角三角函数的定义即可求出AB的值.
解答:解:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=30°,
∴AD=CD=60m,
在Rt△ABD中,
AB=AD•sin∠ADB=60×
=30
(m).
故答案为:30
.
∴∠CAD=30°,
∴AD=CD=60m,
在Rt△ABD中,
AB=AD•sin∠ADB=60×
| ||
| 2 |
| 3 |
故答案为:30
| 3 |
点评:本题考查的是解直角三角形的应用-方向角问题,涉及到三角形外角的性质、等腰三角形的判定与性质、锐角三角函数的定义及特殊角的三角函数值,难度适中.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是( )
| A、任意四边形 |
| B、对角线相等的四边形 |
| C、对角线互相垂直且相等的四边形 |
| D、平行四边形 |
 如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径.已知∠BAC=25°,则∠P的度数为
如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径.已知∠BAC=25°,则∠P的度数为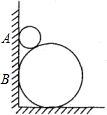 如图,两圆轮叠靠在墙边,如果大圆轮半径R为90cm,AB=60cm,则小圆轮半径r为
如图,两圆轮叠靠在墙边,如果大圆轮半径R为90cm,AB=60cm,则小圆轮半径r为