Question

12．已知直角梯形ABCD中AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，点P从A点出发，沿AD边以1cm/s的速度向点D运动，点Q从点C开始沿CB边以3cm/s的速度向点B运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t．
（1）当t为何值时，四边形PQCD为平行四边形？
（2）某个时刻，四边形PQCD可能是菱形吗？为什么？
（3）当t为何值时，PQ的长度等于10cm？

Answer 1

分析 （1）根据对边平行且相等的四边形是平行四边形列出方程，解方程即可；
（2）根据邻边相等的平行四边形是菱形进行计算，比较邻边的长度得到答案；
（3）分图2和图3两种情况进行分析，运用勾股定理求出FQ的长，列式计算即可．

解答 解：（1）当PD=CQ时，四边形PQCD为平行四边形，
即24-t=3t，
解得，t=6，
故当t=6时，四边形PQCD为平行四边形；
（2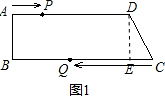）如图1，作DE⊥BC于E，
则四边形ABED为矩形，
∴DE=AB=8，EC=2，
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=2$\sqrt{17}$，
当t=6时，PD=18，
∴PD≠CD，
∴四边形PQCD不可能是菱形；
（3）如图2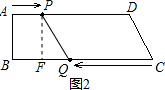，作PF⊥BC于F，
∵PF=8，PQ=10，
∴FQ=$\sqrt{P{Q}^{2}-P{F}^{2}}$=6，
则26-3t-t=6，
解得，t=5；
如图3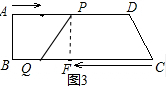，t-（26-3t）=6，
解得，t=8，
∴当t=5或8时，PQ的长度等于10cm．

点评 本题考查的是直角梯形和矩形的性质以及平行四边形、菱形的判定，掌握对边平行且相等的四边形是平行四边形、邻边相等的平行四边形是菱形是就的关键，注意分情况讨论思想的应用．