题目内容
 如图,双曲线y=
如图,双曲线y=| 5 |
| x |
(1)求点A的横坐标a与k的函数表达式;(不写自变量取值范围)
(2)当该直线与双曲线在第一象限的另一交点D的横坐标是9时,求△COD的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把C和A的坐标代入一次函数的解析式,消去b即可求解;
(2)首先求得D的坐标,则线段CD即可求得,作OE⊥AB于点E,根据三角形的面积公式求得OE的长,然后利用三角形的面积公式求解.
(2)首先求得D的坐标,则线段CD即可求得,作OE⊥AB于点E,根据三角形的面积公式求得OE的长,然后利用三角形的面积公式求解.
解答:解:(1)根据题意得:
,
由①得:b=5-k,代入②得:ak+5-k=0,
则:a=
;
(2)在y=
中,令x=9,则y=
,
则D的坐标是(9,
).
则CD=
=
,
根据题意得:
,
解得:
,
则一次函数的解析式是:y=-
x+
,
令x=0,则y=
,即B的坐标是(0,
),
令y=0,则x=10,即A的坐标是(10,0).
则AB=
=
,
 作OE⊥AB于点E.
作OE⊥AB于点E.
则OE=
=
.
S△COD=
CD•OE=
×
×
=
.
|
由①得:b=5-k,代入②得:ak+5-k=0,
则:a=
| k-5 |
| k |
(2)在y=
| 5 |
| x |
| 5 |
| 9 |
则D的坐标是(9,
| 5 |
| 9 |
则CD=
(9-1)2+(
|
8
| ||
| 9 |
根据题意得:
|
解得:
|
则一次函数的解析式是:y=-
| 5 |
| 9 |
| 50 |
| 9 |
令x=0,则y=
| 50 |
| 9 |
| 50 |
| 9 |
令y=0,则x=10,即A的坐标是(10,0).
则AB=
(
|
10
| ||
| 9 |
 作OE⊥AB于点E.
作OE⊥AB于点E.则OE=
| ||||
|
25
| ||
| 13 |
S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 9 |
25
| ||
| 13 |
2
| ||
| 117 |
点评:本题考查了待定系数法求函数的解析式,以及三角形的面积的计算,正确求得OE的长是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
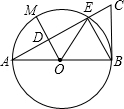 如图,AB为⊙O的直径,AC交⊙O于点E,OM⊥AC,交AC于点D,∠A=35°,AD=2,AC=6.
如图,AB为⊙O的直径,AC交⊙O于点E,OM⊥AC,交AC于点D,∠A=35°,AD=2,AC=6. 如图在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=2,∠ACD=60°,四边形ABCD的面积等于
如图在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=2,∠ACD=60°,四边形ABCD的面积等于 如图,四边形ABCD中,AB=AD,BC=CD,AC,BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注字母,不写推理过程,只要求写出四个你认为正确的结论)?
如图,四边形ABCD中,AB=AD,BC=CD,AC,BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注字母,不写推理过程,只要求写出四个你认为正确的结论)? 如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为
如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为 在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由.
在正方形ABCD中,E是AD的中点,点F在DC上,且DF:FC=1:3,试判断△BEF的形状,并说明理由.