题目内容
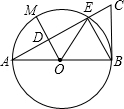 如图,AB为⊙O的直径,AC交⊙O于点E,OM⊥AC,交AC于点D,∠A=35°,AD=2,AC=6.
如图,AB为⊙O的直径,AC交⊙O于点E,OM⊥AC,交AC于点D,∠A=35°,AD=2,AC=6.(1)求∠BOE的度数;
(2)若BC是⊙O的切线,求⊙O的直径AB的长.
考点:切线的性质,圆周角定理
专题:
分析:(1)由圆的性质可知AO=OE,所以∠OAE=∠OEA,再由三角形外角和定理即可求出∠BOE的度数;
(2)已知△ADO∽△ABC,根据相似三角形的性质:对应边的比值相等即可求出⊙O的直径AB的长.
(2)已知△ADO∽△ABC,根据相似三角形的性质:对应边的比值相等即可求出⊙O的直径AB的长.
解答:解:(1)∵AO=OE,
∴∠OAE=∠OEA=35°,
∴∠BOE=2×35°=70°;
(2)∵BC是⊙O的切线,AB为⊙O的直径,
∴∠ABC=90°,
∵OM⊥AC,
∴∠ADO=90°,
∴∠ABC=∠ADO,
∵∠A=∠A,
∴△ADO∽△ABC,
∴AD:AB=AO:AC,
∴2:2AO=AO:6,
∴AO=
.
∴∠OAE=∠OEA=35°,
∴∠BOE=2×35°=70°;

(2)∵BC是⊙O的切线,AB为⊙O的直径,
∴∠ABC=90°,
∵OM⊥AC,
∴∠ADO=90°,
∴∠ABC=∠ADO,
∵∠A=∠A,
∴△ADO∽△ABC,
∴AD:AB=AO:AC,
∴2:2AO=AO:6,
∴AO=
| 6 |
点评:本题考查了切线的性质,圆的性质,相似三角形的判定和性质,题目的综合性较强,难度不大,是中考常见题型.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为
如图,在直角△ACB中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可由△ABC绕点C顺时针旋转得到,其中A′与A是对应点,点B′与B是对应点,点A、B、A′在同一条直线上,则A′B长为下列说法中不正确的是( )
| A、由两条射线所组成的图形叫角 |
| B、∠AOB的顶点是点O |
| C、∠AOB和∠BOA表示同一个角 |
| D、角可以看做一条射线绕着端点旋转到加一个位置所形成的图形 |
 如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF.
如图,已知△ABC和△BDE都为等腰直角三角形,点E在AB上,点F为CD的中点,连接BF. 如图,双曲线y=
如图,双曲线y=