Question

20．矩形ABCD的周长为56，对角线AC，BD交于点O，△ABO与△BCO的周长差为4，则AB的长是（　　）

• A． 12
• B． 22
• C． 16
• D． 26

Answer 1

分析 由矩形的性质得出AB=CD，AD=BC，OA=OB=OC=OD，再由已知条件得出AB+BC=28①，AB-BC=4②，由①+②求出AB即可．

解答 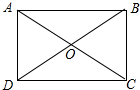解：如图所示：
∵四边形ABCD是矩形，
∴AB=CD，AD=BC，OA=OC=$\frac{1}{2}$AC，OB=OD=$\frac{1}{2}$BD，AC=BD，
∴OA=OB=OC=OD，
∵矩形ABCD的周长为56，
∴AB+BC+CD+AD=56，
∴AB+BC=28①，
∵△ABO与△BCO的周长差为4，
∴（AB+OA+OB）-（OB+OC+BC）=4，
∴AB-BC=4②，
①+②得：2AB=32，
∴AB=16；
故选：C．

点评 本题考查了矩形的性质、矩形周长以及三角形周长的计算；熟练掌握进行的性质，并能进行推理计算是解决问题的关键．