题目内容
如图,矩形OABC的顶点B的坐标为(1,2),反比例函数y=
(0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.

(1)若点E是AB的中点,则m= ,S△OEF= ;
(2)若S△OEF=2S△BEF,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得△MFE≌△BFE?若存在,写出此时点E的坐标;若不存在,说明理由.
| m |
| x |

(1)若点E是AB的中点,则m=
(2)若S△OEF=2S△BEF,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得△MFE≌△BFE?若存在,写出此时点E的坐标;若不存在,说明理由.
考点:反比例函数综合题
专题:综合题
分析:(1)如图1,利用点E为AB的中点易得E点坐标为(1,1),再根据反比例函数图象上点的坐标特征得m=1,则反比例函数解析式为y=
,然后确定F点坐标为(
,2),再利用反比例函数k的几何意义和S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF进行计算;
(2)设E点坐标为(1,m),则F点坐标为(
,2),根据三角形面积公式得到S△BEF=
(1-
)(2-m),根据反比例函数k的几何意义得到S△OFC=S△OAE=
m,由于S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=2-
m-
m-
(1-
)(2-m),则2-
m-
m-
(1-
)(2-m)=2•
(1-
)(2-m),然后解方程求出m即可得到E点坐标;
(3)设E点坐标为(1,m),则F点坐标为(
,2),作EG⊥OC于G,如图2,则CF=
,GE=1,假设△MFE≌△BFE,根据全等的性质得FM=FB=1-
,EM=BE=2-m,∠FME=∠B=90°,再证明Rt△MFC∽Rt△EMG,利用相似比计算出MC=
,MG=m,由于OC=OG+MG+MC=2,则m+m+
=2,解得m=
,于是得到M点的坐标为(1,
).
| 1 |
| x |
| 1 |
| 2 |
(2)设E点坐标为(1,m),则F点坐标为(
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
(3)设E点坐标为(1,m),则F点坐标为(
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
解答: 解:(1)如图1,
解:(1)如图1,
∵矩形OABC的顶点B的坐标为(1,2),点E为AB的中点,
∴E点坐标为(1,1),
∵点E(1,1)在y=
上,
∴m=1×=1,
∴反比例函数解析式为y=
,
把y=2代入得x=
,则F点坐标为(
,2),
∴S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=1×2-
-
-
×1×
=
,
故答案为1,
;
 (2)设E点坐标为(1,m),则F点坐标为(
(2)设E点坐标为(1,m),则F点坐标为(
,2),
则S△BEF=
(1-
)(2-m),S△OFC=S△OAE=
m,
∴S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=2-
m-
m-
(1-
)(2-m),
∵S△OEF=2S△BEF,
∴2-
m-
m-
(1-
)(2-m)=2•
(1-
)(2-m),
整理得
(m-2)2+m-2=0,解得m1=2(舍去),m2=
,
∴E点坐标为(1,
);
(3)存在.理由如下:
设E点坐标为(1,m),则F点坐标为(
,2),作EG⊥OC于G,如图2,则CF=
,GE=1,
∵△MFE≌△BFE,
∴FM=FB=1-
,EM=BE=2-m,∠FME=∠B=90°,
∴∠CMF+∠GME=90°,
而∠CMF+∠MFC=90°,
∴∠MFC=∠GME,
∴Rt△MFC∽Rt△EMG,
∴
=
=
,即
=
=
=
,
∴MC=
,MG=m,
∵OC=OG+MG+MC=2,
∴m+m+
=2,解得m=
,
此时M点的坐标为(1,
).
 解:(1)如图1,
解:(1)如图1,∵矩形OABC的顶点B的坐标为(1,2),点E为AB的中点,
∴E点坐标为(1,1),
∵点E(1,1)在y=
| m |
| x |
∴m=1×=1,
∴反比例函数解析式为y=
| 1 |
| x |
把y=2代入得x=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=1×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为1,
| 3 |
| 4 |
 (2)设E点坐标为(1,m),则F点坐标为(
(2)设E点坐标为(1,m),则F点坐标为(| m |
| 2 |
则S△BEF=
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
∴S△OEF=S矩形ABCO-S△OCF-S△OEA-S△BEF=2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
∵S△OEF=2S△BEF,
∴2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
整理得
| 3 |
| 4 |
| 2 |
| 3 |
∴E点坐标为(1,
| 2 |
| 3 |
(3)存在.理由如下:
设E点坐标为(1,m),则F点坐标为(
| m |
| 2 |
| m |
| 2 |
∵△MFE≌△BFE,
∴FM=FB=1-
| m |
| 2 |
∴∠CMF+∠GME=90°,
而∠CMF+∠MFC=90°,
∴∠MFC=∠GME,
∴Rt△MFC∽Rt△EMG,
∴
| MC |
| GE |
| CF |
| MG |
| MF |
| ME |
| MC |
| 1 |
| ||
| MG |
1-
| ||
| 2-m |
| 1 |
| 2 |
∴MC=
| 1 |
| 2 |
∵OC=OG+MG+MC=2,
∴m+m+
| 1 |
| 2 |
| 3 |
| 4 |
此时M点的坐标为(1,
| 3 |
| 4 |
点评:本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征、反比例函数k的机几何意义和矩形的性质;会运用三角形全等的性质和三角形相似的判定与性质;会利用面积的和差计算不规则图形的面积.

练习册系列答案
相关题目
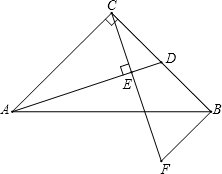 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF. 窗户的形状如图(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长为xcm,计算:
窗户的形状如图(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长为xcm,计算: