题目内容
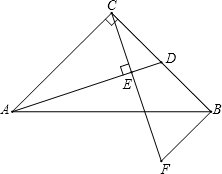 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.考点:全等三角形的判定与性质
专题:证明题
分析:由直角三角形ACD中,CF垂直于AD,利用同角的余角相等得到一对角相等,再由一对直角相等,AC=BC,利用AAS得到三角形ACD与三角形CBF全等,利用全等三角形的对应边相等得到CD=BF,由D为BC中点,得到CD=BD,等量代换即可得证.
解答:证明:∵Rt△ACD中,CE⊥AD,
∴∠BCF+∠F=90°,∠BCF+∠ADC=90°,
∴∠F=∠ADC,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(AAS),
∴CD=BF,
∵D为BC中点,
∴CD=BD,
∴BF=CD=BD=
BC=
AC,
则AC=2BF.
∴∠BCF+∠F=90°,∠BCF+∠ADC=90°,
∴∠F=∠ADC,
在△ACD和△CBF中,
|
∴△ACD≌△CBF(AAS),
∴CD=BF,
∵D为BC中点,
∴CD=BD,
∴BF=CD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
则AC=2BF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
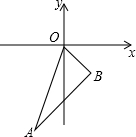 如图,直线OA的解析式为y=3x,点A的横坐标是-1,OB=
如图,直线OA的解析式为y=3x,点A的横坐标是-1,OB=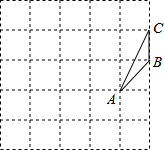 如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?
如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?