题目内容
某机械研究所发出一件新产品,计划生产1200件新产品投放市场试销.准备聘请都具备加工能力的甲、乙两人生产.经过调查,获得如下信息:
信息一:甲单独加工完成这批产品比乙单独加工完成这批产品多用10天;
信息二:乙每天加工的数量是甲每天加工数量的1.5倍.
(1)甲每天可加工这种产品多少件?
(2)为及早开拓市场,公司计划这批产品生产时间不超过15天,决定聘请甲、乙两人同时加工.两人共同加工完若干件后,乙因有事退出,剩下的任务由甲继续单独完成.求两人同时至少要加工完多少件后,才能达到上述预计的时间?
信息一:甲单独加工完成这批产品比乙单独加工完成这批产品多用10天;
信息二:乙每天加工的数量是甲每天加工数量的1.5倍.
(1)甲每天可加工这种产品多少件?
(2)为及早开拓市场,公司计划这批产品生产时间不超过15天,决定聘请甲、乙两人同时加工.两人共同加工完若干件后,乙因有事退出,剩下的任务由甲继续单独完成.求两人同时至少要加工完多少件后,才能达到上述预计的时间?
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)如果设甲工厂每天加工x件产品,那么根据乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍,可知乙工厂每天加工1.5x件产品.然后根据等量关系:甲工厂单独加工完成这批产品的天数-乙工厂单独加工完成这批产品的天数=10列出方程.
(2)设甲、乙共同完成了y件新产品.则由“公司计划这批产品生产时间不超过15天”列出不等式.
(2)设甲、乙共同完成了y件新产品.则由“公司计划这批产品生产时间不超过15天”列出不等式.
解答:解:(1)设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得:x
-
=10,
解得:x=40.
经检验:x=40是原方程的根,且符合题意.
答:甲工厂每天加工40件产品.
(2)由(1)知,甲工厂每天加工40件产品,则乙工厂每天加工40×1.5=60(个)新产品.
设甲、乙共同完成了y件新产品.则
+
≤15,
解得 y≥1000.
故两人同时至少要加工完1000件后,才能达到上述预计的时间.
依题意得:x
| 1200 |
| 1200 |
| 1.5x |
解得:x=40.
经检验:x=40是原方程的根,且符合题意.
答:甲工厂每天加工40件产品.
(2)由(1)知,甲工厂每天加工40件产品,则乙工厂每天加工40×1.5=60(个)新产品.
设甲、乙共同完成了y件新产品.则
| y |
| 60+40 |
| 1200-y |
| 40 |
解得 y≥1000.
故两人同时至少要加工完1000件后,才能达到上述预计的时间.
点评:本题考查了分式方程在实际生产生活中的应用.理解题意找出题中的等量关系,列出方程是解题的关键.注意分式方程一定要验根.

练习册系列答案
相关题目
在下列各式中,能因式分解的是( )
| A、x2+(-y)2 |
| B、4x2+y2 |
| C、-x2+y2 |
| D、x2-y3 |
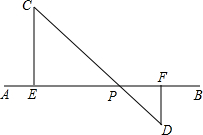 如图,AB是一条河流,要铺设管道将河水引到C、D两个用水点,现有两种铺设管道的方案;
如图,AB是一条河流,要铺设管道将河水引到C、D两个用水点,现有两种铺设管道的方案; 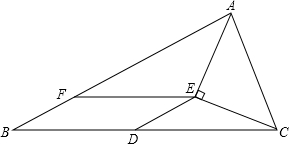 如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,
如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,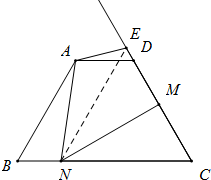 已知,在等腰梯形ABCD中,AD∥BC,AD=2,AB=CD=4,且∠B=60°,M是CD上一动点,作MN⊥CD,交BC于N,将∠C沿MN翻折,使点C落在射线CD上的点E处,当△ANE为等腰三角形时,CM的长为
已知,在等腰梯形ABCD中,AD∥BC,AD=2,AB=CD=4,且∠B=60°,M是CD上一动点,作MN⊥CD,交BC于N,将∠C沿MN翻折,使点C落在射线CD上的点E处,当△ANE为等腰三角形时,CM的长为 如图,图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上.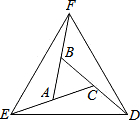 如图,△ABC中,∠BAC=∠ACB=60°,延长△ABC的各边,使BF=AC=AE=CD=AB,顺次连接D、E、F.求证:△DEF是等边三角形.
如图,△ABC中,∠BAC=∠ACB=60°,延长△ABC的各边,使BF=AC=AE=CD=AB,顺次连接D、E、F.求证:△DEF是等边三角形.