题目内容
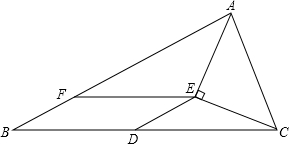 如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,
如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,求证:四边形BDEF是平行四边形.
考点:平行四边形的判定
专题:证明题
分析:延长CE交AB于M,证两三角形全等,推出E为CM中点,根据三角形中位线推出DE∥AB,根据平行四边形的判定推出即可.
解答:证明:
延长CE交AB于M,
∵AE⊥CE,
∴∠AEC=∠AEM=90°,
∵AE是∠BAC的平分线,
∴∠MAE=∠CAE,
在△MAE和△CAE中,
,
∴△MAE≌△CAE(ASA),
∴CE=EM,
∵D为BC中点,
∴DE∥AB,
∵EF∥BC,
∴四边形BDEF是平行四边形.

延长CE交AB于M,
∵AE⊥CE,
∴∠AEC=∠AEM=90°,
∵AE是∠BAC的平分线,
∴∠MAE=∠CAE,
在△MAE和△CAE中,
|
∴△MAE≌△CAE(ASA),
∴CE=EM,
∵D为BC中点,
∴DE∥AB,
∵EF∥BC,
∴四边形BDEF是平行四边形.
点评:本题考查了全等三角形的性质和判定,三角形的中位线,平行四边形的判定的应用,注意:有两组对边分别平行的四边形是平行四边形.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
若二次函数y=mxm2-m-4+2x的图象开口向下,则一次函数y=(m+3)x-m的图象一定不经过的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在Rt△ABC中,∠C=90°,BC:AC=1:2,AB=5,则斜边AB上的高为( )
A、
| ||||
| B、2 | ||||
| C、1 | ||||
D、
|
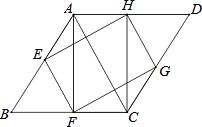 已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE.
已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE. 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.