题目内容
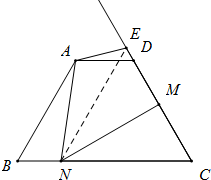 已知,在等腰梯形ABCD中,AD∥BC,AD=2,AB=CD=4,且∠B=60°,M是CD上一动点,作MN⊥CD,交BC于N,将∠C沿MN翻折,使点C落在射线CD上的点E处,当△ANE为等腰三角形时,CM的长为
已知,在等腰梯形ABCD中,AD∥BC,AD=2,AB=CD=4,且∠B=60°,M是CD上一动点,作MN⊥CD,交BC于N,将∠C沿MN翻折,使点C落在射线CD上的点E处,当△ANE为等腰三角形时,CM的长为考点:等腰梯形的性质,等腰三角形的判定,翻折变换(折叠问题)
专题:
分析:利用等腰梯形的性质以及勾股定理得出AN2=AG2+GN2=12+(4-2x)2,AE2=AH2+EH2=3+(5-2x)2,进而利用①令AN=NE时;②令AE=NE;③令AN=AE分别求出即可.
解答: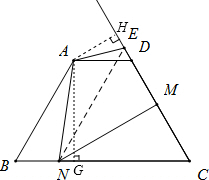 解:过A作AG⊥BC,交BC于G,过A点作AH⊥CD,交CD的延长线于H.设MC=x
解:过A作AG⊥BC,交BC于G,过A点作AH⊥CD,交CD的延长线于H.设MC=x
∵∠B=60°,四边形ABCD为等腰梯形,
∴∠C=60°,NC=NE=2x
BG=
AB=2,AG=
=2
,BC=6,
GN=4-2x,
AN2=AG2+GN2=12+(4-2x)2
∵AD∥BC,
∴∠ADH=∠C=60°
DH=
AD=1,AH=
,HE=5-2x,AE2=AH2+EH2=3+(5-2x)2
①令AN=NE时 12+(4-2x)2=(2x)2
解得:x=
;
②令AE=NE,
则3+(5-2x)2=(2x)2
解得:x=
;
③令AN=AE
则 12+(4-2x)2=3+(5-2x)2
解得x=0(不合题意)
故当三角形ANE为等腰三角形时,CM的长为
或
.
故答案为:
或
.
 解:过A作AG⊥BC,交BC于G,过A点作AH⊥CD,交CD的延长线于H.设MC=x
解:过A作AG⊥BC,交BC于G,过A点作AH⊥CD,交CD的延长线于H.设MC=x∵∠B=60°,四边形ABCD为等腰梯形,
∴∠C=60°,NC=NE=2x
BG=
| 1 |
| 2 |
| AB2-BF2 |
| 3 |
GN=4-2x,
AN2=AG2+GN2=12+(4-2x)2
∵AD∥BC,
∴∠ADH=∠C=60°
DH=
| 1 |
| 2 |
| 3 |
①令AN=NE时 12+(4-2x)2=(2x)2
解得:x=
| 7 |
| 4 |
②令AE=NE,
则3+(5-2x)2=(2x)2
解得:x=
| 7 |
| 5 |
③令AN=AE
则 12+(4-2x)2=3+(5-2x)2
解得x=0(不合题意)
故当三角形ANE为等腰三角形时,CM的长为
| 7 |
| 4 |
| 7 |
| 5 |
故答案为:
| 7 |
| 4 |
| 7 |
| 5 |
点评:此题主要考查了等腰梯形的性质以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 在△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC等于( )
在△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC等于( )| A、2:1 | B、1:2 |
| C、3:2 | D、2:3 |
在Rt△ABC中,∠C=90°,BC:AC=1:2,AB=5,则斜边AB上的高为( )
A、
| ||||
| B、2 | ||||
| C、1 | ||||
D、
|
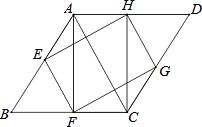 已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE.
已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE. 如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是
如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是