题目内容
17.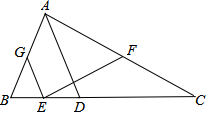 如图,在△ABC中,点D在边BC上,AB=AD,E是BD的中点,F是AC的中点.
如图,在△ABC中,点D在边BC上,AB=AD,E是BD的中点,F是AC的中点.(1)求证:EF=$\frac{1}{2}$AC;
(2)若点G是边AB的中点,连接EG,线段GE与EF能否相等?说明理由.
分析 (1)连接AE,根据等腰三角形的性质得到AE⊥BD,根据直角三角形的性质得到EF=$\frac{1}{2}$AC;
(2)根据三角形准确性定理得到EG=$\frac{1}{2}$AD,根据(1)的结论解答即可.
解答 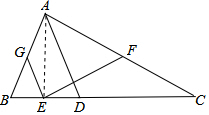 (1)证明:连接AE,
(1)证明:连接AE,
∵AB=AD,E是BD的中点,
∴AE⊥BD,
∵F是AC的中点,
∴EF=$\frac{1}{2}$AC;
(2)∵点G是边AB的中点,E是BD的中点,
∴EG=$\frac{1}{2}$AD,又AB=AD,
∴EG=$\frac{1}{2}$AB,
∴当AB=AC时,GE=EF.
点评 本题考查的是直角三角形的性质、等腰三角形的性质、三角形中位线定理的应用,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
6. 如图,⊙O的直径AB=2,点C在⊙O上,弦AC=1,则∠D的度数是( )
如图,⊙O的直径AB=2,点C在⊙O上,弦AC=1,则∠D的度数是( )
 如图,⊙O的直径AB=2,点C在⊙O上,弦AC=1,则∠D的度数是( )
如图,⊙O的直径AB=2,点C在⊙O上,弦AC=1,则∠D的度数是( )| A. | 30° | B. | 60° | C. | 45° | D. | 75° |
7.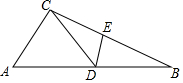 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )| A. | 45° | B. | 50° | C. | 51° | D. | 52° |
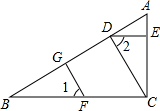 如图,已知DE⊥AC于E点,BC⊥AC于点C,FG⊥AB于G点,∠1=∠2,求证:CD⊥AB.
如图,已知DE⊥AC于E点,BC⊥AC于点C,FG⊥AB于G点,∠1=∠2,求证:CD⊥AB. 如图,AD⊥BC,∠1=∠2,∠C=55°.求∠BAC的度数.
如图,AD⊥BC,∠1=∠2,∠C=55°.求∠BAC的度数. 如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.
如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.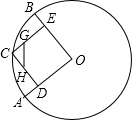 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E,点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上顺时针运动时,已知⊙O的半径长为6,则GH的长度为( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E,点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上顺时针运动时,已知⊙O的半径长为6,则GH的长度为( )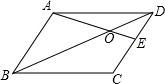 如图,在?ABCD中,E为DC边上的一点,AE交BD于点O,若OD=3,BD=9,求证:DE=CE.
如图,在?ABCD中,E为DC边上的一点,AE交BD于点O,若OD=3,BD=9,求证:DE=CE.