题目内容
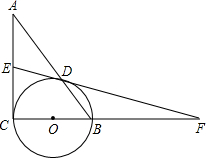 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交斜边AB于点D,E为AC上一点,延长ED、CB交于F点,且∠A+∠F=∠ABC.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交斜边AB于点D,E为AC上一点,延长ED、CB交于F点,且∠A+∠F=∠ABC.(1)求证:直线EF为⊙O的切线;
(2)若tan∠A=
| 3 |
| 4 |
考点:切线的判定,解直角三角形
专题:证明题
分析:(1)连OD、DC,根据圆周角定理的推论由BC为直径得到∠BDC=90°,则∠ADC=90°,根据三角形外角∠ABC=∠F+∠BDF,而∠A+∠F=∠ABC,则∠BDF=∠A,根据等角的余角相等得到∠ECD=∠EDC,而∠ECD+∠OCD=90°,易得∠EDC+∠ODC=∠ECD+∠OCD=90°,根据切线的判定定理即可得到结论;
(2)过D作DH⊥BC于H,根据等角的余角相等得到∠ODH=∠F,∠A=∠DCB,在Rt△BCD中,tan∠DCB=
,不妨设DB=3x,CD=4x,利用勾股定理可计算出BC=5x,即半径为
x,利用面积公式可计算出OH=
x,在Rt△ODH中,利用勾股定理计算出OH=
x,然后根据正切的定义得到tan∠ODH=
=
,即可得到tan∠F的值.
(2)过D作DH⊥BC于H,根据等角的余角相等得到∠ODH=∠F,∠A=∠DCB,在Rt△BCD中,tan∠DCB=
| DB |
| CD |
| 5 |
| 2 |
| 12 |
| 5 |
| 7 |
| 10 |
| OH |
| DH |
| 7 |
| 24 |
解答:(1) 证明:连OD、DC,如图,
证明:连OD、DC,如图,
∵BC为直径,
∴∠BDC=90°,
∴∠ADC=90°,
∵∠ABC=∠F+∠BDF,
而∠A+∠F=∠ABC,
∴∠BDF=∠A,
又∵∠BDF=∠ADE,
∴∠A=∠ADE,
而∠ECD+∠A=∠EDC+∠ADE=90°,
∴∠ECD=∠EDC,
而∠ACB=90°,OD=OC,
∴∠EDC+∠ODC=∠ECD+∠OCD=90°,
∴直线EF为⊙O的切线;
(2)解:过D作DH⊥BC于H,如图,
∵∠ODH+∠DOB=90°,∠F+∠DOB=90°,
∴∠ODH=∠F,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°,
∴∠A=∠DCB,
在Rt△BCD中,tan∠DCB=
,
而tan∠A=
,
不妨设DB=3x,CD=4x,
BC=
=5x,
∴OC=
x,
∵
OH•BC=
CD•BD,
∴OH=
x,
在Rt△ODH中,OH=
=
) 2=
x,
∴tan∠ODH=
=
=
,
∴tan∠F=
.
 证明:连OD、DC,如图,
证明:连OD、DC,如图,∵BC为直径,
∴∠BDC=90°,
∴∠ADC=90°,
∵∠ABC=∠F+∠BDF,
而∠A+∠F=∠ABC,
∴∠BDF=∠A,
又∵∠BDF=∠ADE,
∴∠A=∠ADE,
而∠ECD+∠A=∠EDC+∠ADE=90°,
∴∠ECD=∠EDC,
而∠ACB=90°,OD=OC,
∴∠EDC+∠ODC=∠ECD+∠OCD=90°,
∴直线EF为⊙O的切线;
(2)解:过D作DH⊥BC于H,如图,
∵∠ODH+∠DOB=90°,∠F+∠DOB=90°,
∴∠ODH=∠F,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°,
∴∠A=∠DCB,
在Rt△BCD中,tan∠DCB=
| DB |
| CD |
而tan∠A=
| 3 |
| 4 |
不妨设DB=3x,CD=4x,
BC=
| CD2+BD2 |
∴OC=
| 5 |
| 2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OH=
| 12 |
| 5 |
在Rt△ODH中,OH=
| OC2-OH2 |
(
|
| 7 |
| 10 |
∴tan∠ODH=
| OH |
| DH |
| ||
|
| 7 |
| 24 |
∴tan∠F=
| 7 |
| 24 |
点评:本题考查了切线的判定:经过半径的外端点,并且与半径垂直的直线是圆的切线.也考查了圆周角定理的推论以及解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在反比例函数y=
的图象上的点是( )
| 3 |
| x |
| A、(1,-2) |
| B、(1,2) |
| C、(1,-3) |
| D、(1,3 ) |
 如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=
如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=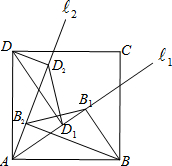 如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由.
如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由. 如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=
如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=