题目内容
 如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=
如图,先将正方形ABCD沿EF对折使AB与DC完全重合,再将角D翻折,使点D落在EF上,折痕为CG,那么∠DCG=考点:翻折变换(折叠问题)
专题:数形结合
分析:根据折叠的性质可得CF=
BC=
DC,DC=CD',从而可求出∠CD'F=30°,∠DCD'=30°,也可得出∠DCG的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由折叠的性质得,CF=
BC=
DC,DC=CD',
故在直角三角形CD'F中可得出,∠CD'F=30°,
∵DC∥EF,
∴∠DCD'=30°,
由折叠的性质得,∠DCG=∠D'CG=
∠DCD'=15°.
故答案为:15°.
| 1 |
| 2 |
| 1 |
| 2 |
故在直角三角形CD'F中可得出,∠CD'F=30°,
∵DC∥EF,
∴∠DCD'=30°,
由折叠的性质得,∠DCG=∠D'CG=
| 1 |
| 2 |
故答案为:15°.
点评:此题考查了折叠的性质及含30°角的直角三角形的性质,解答本题的关键是掌握翻折前后对应线段相等,对应角相等,难度一般.

练习册系列答案
相关题目
下列事件中,不是随机事件的是( )
| A、某射击运动员,在练习射击中,一共射击50次,其中有10次击中靶心 |
| B、小明从一副扑克牌中抽取一张,结果他抽的是大王 |
| C、从装有黑、白各3颗围棋子的袋中抽取4颗,结果有黑白两种棋子 |
| D、同时抛掷两枚质地均匀的骰子一次,结果点数之和是6 |

 如图,点M、P、N在同一直线上,△AMP、△BPN均为等边三角形,MB、NA相交于Q,则∠AQM=
如图,点M、P、N在同一直线上,△AMP、△BPN均为等边三角形,MB、NA相交于Q,则∠AQM=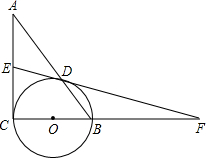 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交斜边AB于点D,E为AC上一点,延长ED、CB交于F点,且∠A+∠F=∠ABC.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O交斜边AB于点D,E为AC上一点,延长ED、CB交于F点,且∠A+∠F=∠ABC.