题目内容
已知Rt△ABC外接圆半径为
，直角边AC=3，则Rt△ABC内切圆半径为 ．
| 5 |
| 2 |
考点：三角形的内切圆与内心,三角形的外接圆与外心
专题：
分析：利用直角三角形斜边长为外接圆直径，由勾股定理得出BC=4，再根据三角形的面积等于周长乘以半径的一半，从而得出三角形内切圆半径．
解答：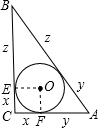
解：∵Rt△ABC外接圆半径为
，
∴Rt△ABC斜边长度为5，
∵直角边AC=3，
∴BC=
=4；
设三角形内切圆半径为r，则：
×r×（5+4+3）=
×3×4，
r=1．
故答案为：1．
解：∵Rt△ABC外接圆半径为| 5 |
| 2 |
∴Rt△ABC斜边长度为5，
∵直角边AC=3，
∴BC=
| 52-32 |
设三角形内切圆半径为r，则：
| 1 |
| 2 |
| 1 |
| 2 |
r=1．
故答案为：1．
点评：此题主要考查了三角形内切圆的性质以及直角三角形外接圆的性质，根据已知得出三角形三边长度是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，点M、P、N在同一直线上，△AMP、△BPN均为等边三角形，MB、NA相交于Q，则∠AQM=下面方程组中，解是
的二元一次方程组是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
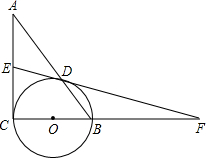如图，在Rt△ABC中，∠ACB=90°，以BC为直径作⊙O交斜边AB于点D，E为AC上一点，延长ED、CB交于F点，且∠A+∠F=∠ABC．
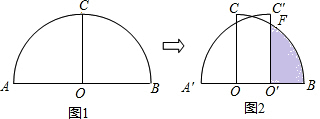
△ABC、△A1B1C1在平面直角坐标系位置如图（方格小正方形的边长为1）