题目内容
17.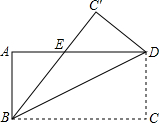 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )
如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先根据翻折变换的性质得出CD=C′D,∠C=∠C′=90°,再设DE=x,则AE=8-x,由全等三角形的判定定理得出Rt△ABE≌Rt△C′DE,可得出BE=DE=x,在Rt△ABE中利用勾股定理即可求出x的值,进而得出DE的长.
解答 解:∵Rt△DC′B由Rt△DBC翻折而成,
∴CD=C′D=AB=8,∠C=∠C′=90°,
设DE=x,则AE=8-x,
∵∠A=∠C′=90°,∠AEB=∠DEC′,
∴∠ABE=∠C′DE,
在Rt△ABE与Rt△C′DE中,
$\left\{\begin{array}{l}{∠A=∠C′=90°}\\{AB=C′D}\\{∠ABE=∠C′DE}\end{array}\right.$,
∴Rt△ABE≌Rt△C′DE(ASA),
∴BE=DE=x,
在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得:x=5,
∴DE的长为5.
故选C.
点评 本题考查的是翻折变换的性质及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.一组数据:5,7,4,9,7的中位数和众数分别是( )
| A. | 4,7 | B. | 7,7 | C. | 4,4 | D. | 4,5 |
8.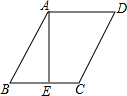 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )| A. | $12-6\sqrt{2}$ | B. | $6\sqrt{2}+12$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
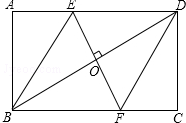 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.
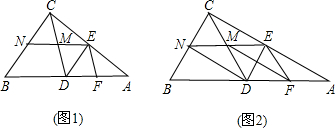
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.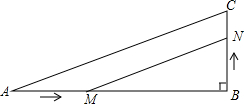 如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.
如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.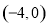 ,B
,B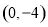 ,C
,C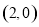 三点.
三点. 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.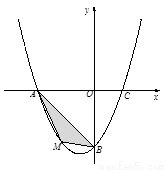
 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.
如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.