题目内容
6.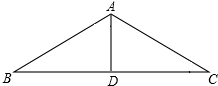 如图,在△ABC中,AB=AC,其周长为16,AD为BC边上的高,AD=4,求∠B的正弦值.
如图,在△ABC中,AB=AC,其周长为16,AD为BC边上的高,AD=4,求∠B的正弦值.
分析 根据AD⊥BC,将等腰三角形转化为直角三角形,利用勾股定理求BD,利用锐角三角函数的定义求∠B的正弦值.
解答 解:∵AB=AC,AD⊥BC,
∴BD=CD,
在Rt△ABD中,设AB=x,则BD=8-x,
由勾股定理,得AD2+BD2=AB2,
∵AD=4,
∴16+(8-x)2=x2,
解得x=5,
由锐角三角函数的定义,得sinB=$\frac{AD}{AB}$=$\frac{4}{5}$.
点评 本题考查了勾股定理,等腰三角形的性质,三角函数的应用,关键是将问题转化到直角三角形中求解,并且要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
11.计算(a+2b)2的结果是( )
| A. | a2+4b2 | B. | a2+2ab+2b2 | C. | a2+4ab+2b2 | D. | a2+4ab+4b2 |
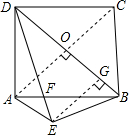 正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE.
正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE.