题目内容
16.(1)-15-(-8)+(-11)-12;(2)$(-\frac{7}{2})×(\frac{1}{6}-\frac{1}{2})×\frac{3}{14}÷(-\frac{1}{2})$;
(3)(-2)2+4×(-3)2-(-4)2÷(-2);
(4)-5m2n+4mn2-2mn+6m2n+3mn;
(5)$-\frac{1}{3}ab-\frac{1}{2}{a^2}+\frac{1}{3}{a^2}-(-\frac{2}{3}ab)$;
(6)$4{x^2}-[\frac{3}{2}x-(\frac{1}{2}x-3)+3{x^2}]$.
分析 (1)先化简,再分类计算即可;
(2)先算括号里面的减法,把除法改为乘法计算即可;
(3)先算乘方,再算乘除,最后算加减;
(4)直接合并同类项即可;
(5)(6)先去括号,再进一步合并同类项即可.
解答 解:(1)-15+8-11-12
=-30;
(2)原式=(-$\frac{7}{2}$)×(-$\frac{1}{3}$)×$\frac{3}{14}$×(-2)
=-$\frac{1}{2}$;
(3)原式=4+4×9-16÷(-2)
=4+36+8
=48;
(4)原式=(-5m2n+6m2n)+(-2mn+3mn)+4mn2
=m2n+mn+4mn2;
(5)原式=$-\frac{1}{3}ab-\frac{1}{2}{a^2}+\frac{1}{3}{a^2}+\frac{2}{3}ab$
=$(-\frac{1}{3}ab+\frac{2}{3}ab)+(-\frac{1}{2}{a^2}+\frac{1}{3}{a^2})$
=$\frac{1}{3}ab-\frac{1}{6}{a^2}$;
(6)原式=$4{x^2}-[\frac{3}{2}x-\frac{1}{2}x+3+3{x^2}]$
=$4{x^2}-\frac{3}{2}x+\frac{1}{2}x-3-3{x^2}$…(
=$(4{x^2}-3{x^2})+(-\frac{3}{2}x+\frac{1}{2}x)-3$
=x2-x-3.
点评 此题考查有理数的混合运算,整式的混合运算,正确判定运算符号,理清运算顺序计算即可.

练习册系列答案
相关题目

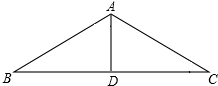 如图,在△ABC中,AB=AC,其周长为16,AD为BC边上的高,AD=4,求∠B的正弦值.
如图,在△ABC中,AB=AC,其周长为16,AD为BC边上的高,AD=4,求∠B的正弦值.