题目内容
20.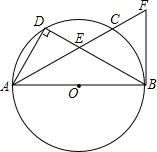 如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.
如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.(1)求⊙O的直径;
(2)猜想△BEF的形状,并证明你的猜想.
分析 (1)由AB是⊙O的直径,得到∠D=90°,由于点D是$\widehat{AC}$的中点,根据圆周角定理得到∠DAB=∠ABD,证得△ADE∽△BDA,得到比例式$\frac{AD}{BD}$=$\frac{DE}{AD}$,然后根据勾股定理即可求得结论;
(2)在Rt△ABD中,tan∠ABD=$\frac{AD}{BD}$=$\frac{\sqrt{3}}{3}$,得到∠ABD=30°,根据BF是⊙O的切线,求出∠ABF=90°得到∠F=∠EBF=60°,即可得到结果.
解答 解:(1)∵AB是⊙O的直径,
∴∠D=90°,
∵点D是$\widehat{AC}$的中点,
∴∠DAB=∠ABD,
∴△ADE∽△BDA,
∴$\frac{AD}{BD}$=$\frac{DE}{AD}$,
∴AD2=BD•DE,
∵DE=4,BE=8,
∴AD=4$\sqrt{3}$,
∴AB=$\sqrt{{AD}^{2}{+BD}^{2}}$=8$\sqrt{3}$;
(2)在Rt△ABD中,tan∠ABD=$\frac{AD}{BD}$=$\frac{\sqrt{3}}{3}$,
∴∠ABD=30°,
∴∠DAE=∠ABD=30°,
∵BF是⊙O的切线,
∴∠ABF=90°
∴∠F=∠EBF=60°,
∴△BEF是等边三角形.
点评 本题考查了切线的性质,圆周角定理,勾股定理,相似三角形的判定和性质,证得△ADE∽△BDA是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )| A. | 36° | B. | 70° | C. | 72° | D. | 108° |
9.下列运算,正确的是( )
| A. | 4a-2a=2 | B. | a6÷a3=a2 | C. | (-a3b)2=a6b2 | D. | (a+b)2=a2+b2 |
10.菱形的两条对角线长分别为6和8,则菱形的面积是( )
| A. | 10 | B. | 20 | C. | 24 | D. | 48 |
 如图,已知△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,BD=AD,DE=DC,求证:BF⊥AC.
如图,已知△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,BD=AD,DE=DC,求证:BF⊥AC.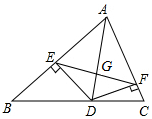 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.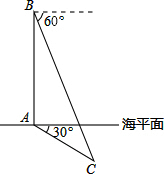 在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方
在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方