题目内容
6.在一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.(1)若从中任意摸出一个球,求摸出红球的概率.
(2)若摸出1个球,记下颜色后不放回,再摸出1个球,求两次摸出的球恰好颜色不同的概率(画树状图或列表说明)
分析 (1)直接利用概率公式计算即可;
(2)画出树形图得到所有可能结果,即可求出两次摸出的球恰好颜色不同的概率.
解答 解:
(1)∵一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同,
∴摸出1个球是白球的概率是:$\frac{2}{4}$=$\frac{1}{2}$;
(2)画树状图得: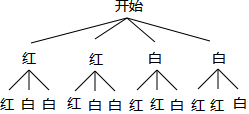
∵共有12种等可能的结果,两次摸出的球恰好颜色不同有8种情况,
∴两次摸出的球恰好颜色不同的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14.不等式组$\left\{\begin{array}{l}{-3x>-6}\\{2x+1>0}\end{array}\right.$的解集是( )
| A. | x>2 | B. | x<-$\frac{1}{2}$ | C. | -$\frac{1}{2}$<x<2 | D. | $\frac{1}{2}$<x<2 |
1.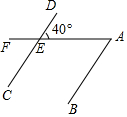 如图,直线AB∥CD,AF交CD于点E,∠DEF=140°,则∠A的度数是( )
如图,直线AB∥CD,AF交CD于点E,∠DEF=140°,则∠A的度数是( )
 如图,直线AB∥CD,AF交CD于点E,∠DEF=140°,则∠A的度数是( )
如图,直线AB∥CD,AF交CD于点E,∠DEF=140°,则∠A的度数是( )| A. | 140° | B. | 40° | C. | 50° | D. | 60° |

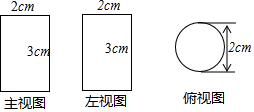 如图为一个几何体的三视图,
如图为一个几何体的三视图,