题目内容
已知关于x的方程x2+（1﹣m）x+
=0有两个不相等的实数根，则m的最大整数值是 ．
0．
【解析】
试题分析：根据方程有两个不相等的实数根可知△＞0，据此求出m的取值范围，从而得到m的最大整数值．
试题解析：∵关于x的方程x2+（1-m）x+
=0有两个不相等的实数根，
∴△＞0，
∴（1-m）2-4×1×＞0，
∴（1-m）2-m2＞0，
∴1+m2-2m-m2＞0，
∴1-2m＞0，
解得，m＜
，
故m的最大整数值是0．
考点：根的判别式．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
，该双曲线位于第一、三象限的概率是 ．
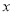，根据题意，可得方程_______________．
D.30米