题目内容
关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实数根x1、x2,且有x1+x2-x1·x2=1-a,求a的值.
-1.
【解析】
试题分析:由关于x的方程有两个不相等的实数根,得到根的判别式的值大于0列出关于a的不等式,求出不等式的解集得到a的范围,再利用根与系数的关系表示出两根之和与两根之积,代入已知的等式中得到关于a的方程,求出方程的解即可得到a的值.
试题解析:∵关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,
∴△=(3a+1)2-8a(a+1)>0,即9a2+6a+1-8a2-8a=a2-2a+1=(a-1)2>0,即a≠1,a≠0,
且x1+x2= ,x1x2=
,x1x2=
∴x1-x1x2+x2= =1-a,
=1-a,
即
∵a≠1,即a-1≠0,
∴a=-1.
考点:1.根的判别式;2.一元二次方程的定义;3.根与系数的关系.

练习册系列答案
相关题目


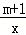 在每个象限内的函数值y随x的增大而增大,则m的取值范围是( )
在每个象限内的函数值y随x的增大而增大,则m的取值范围是( )
 =0有两个不相等的实数根,则m的最大整数值是 .
=0有两个不相等的实数根,则m的最大整数值是 .
 与
与 是同类项,则
是同类项,则 .
.