题目内容
8.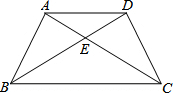 如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC.(1)求证:△ABE≌△DCE;
(2)连接AD,判断AD和BC的位置关系,并证明之.
分析 (1)利用“SAS”可证明△ABC≌△DCB,则∠ACB=∠DBC,从而得到∠ABE=∠DCE,然后根据“AAS”可判断△ABE≌△DCE;
(2)先利用△ABE≌△DCE得到AE=DE,根据等腰三角形的判定与三角形内角和得到∠EAD=∠EDA=$\frac{1}{2}$(180°-∠AED),∠EBC=$\frac{1}{2}$(180°-∠BEC),则利用∠AED=∠BEC得到∠EDA=∠EBC,然后根据平行线的判定方法可判断AD∥BC.
解答 (1)证明:在△ABC和△DCB中
$\left\{\begin{array}{l}{AB=DC}\\{∠ABC=∠DCB}\\{BC=CB}\end{array}\right.$
∴△ABC≌△DCB,
∴∠ACB=∠DBC,
∴∠ABE=∠DCE,
在△ABE和△DCE中
$\left\{\begin{array}{l}{∠AEB=∠DEC}\\{∠ABE=∠DCE}\\{AB=DC}\end{array}\right.$
∴△ABE≌△DCE;
(2)解:AD∥BC.理由如下:
由(1)知,△ABE≌△DCE,
∴AE=DE,
∴∠EAD=∠EDA=$\frac{1}{2}$(180°-∠AED),
∵∠ABE=∠DCE,
∴∠EBC=$\frac{1}{2}$(180°-∠BEC),
而∠AED=∠BEC,
∴∠EDA=∠EBC,
∴AD∥BC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
16.下列说法正确的是( )
| A. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线相交所成的四个角相等,则这两条直线互相垂直 | |
| D. | 相等的两个角是对顶角 |
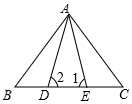 已知如图所示,∠1=∠2,∠B=∠C,BD=CE;写出图中全等的三角形是△ABD≌△ACE;△ABE≌△ACD.
已知如图所示,∠1=∠2,∠B=∠C,BD=CE;写出图中全等的三角形是△ABD≌△ACE;△ABE≌△ACD.
 如图,△ABC三边的中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分面积是( )
如图,△ABC三边的中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分面积是( ) 如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.
如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.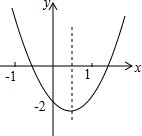 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( ) 如图,在平面直角坐标系中,点M在第二象限.
如图,在平面直角坐标系中,点M在第二象限.