题目内容
18.(1)解方程组$\left\{\begin{array}{l}{4(x+3)+5(y-1)=0①}\\{2x+3(y+2)=3②}\end{array}\right.$(2)解方程组$\left\{\begin{array}{l}{\frac{x-3}{2}=\frac{y+1}{3}①}\\{\frac{2}{3}(x-1)+\frac{y}{3}=1②}\end{array}\right.$;
(3)解不等式组$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{2}+1≥\frac{x+1}{2}②}\end{array}\right.$.
分析 (1)将方程组整理成一般式后,利用加减消元法求解可得;
(2)将方程组整理成一般式后,利用加减消元法求解可得;
(3)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原方程组整理可得:$\left\{\begin{array}{l}{4x+5y=-7}&{③}\\{2x+3y=-3}&{④}\end{array}\right.$,
④×2-①,得:y=1,
将y=1代入③,得:4x+5=-7,
解得:x=-3,
∴方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$;
(2)原方程整理可得$\left\{\begin{array}{l}{3x-2y=11}&{③}\\{2x+y=5}&{④}\end{array}\right.$,
③+④×2,得:7x=21,
解得:x=3,
将x=3代入④,得:y=-1,
∴方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(3)解不等式①,得:x≤1,
解不等式②,得:x≥0,
则不等式组的解集为0≤x≤1.
点评 本题主要考查解二元一次方程组和一元一次不等式组的能力,熟练掌握加减消元法解方程组和正确求出每一个不等式解集是解答此题的关键.

练习册系列答案
相关题目
6. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
 如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )| A. | 24 | B. | 26 | C. | 30 | D. | 48 |
3.实数$\frac{1}{3}$、$\sqrt{3}$、π、$\sqrt{16}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.若a、b是有理数,且|a|=1,|b|=2,ab<0,则a+b=( )
| A. | 1或-3 | B. | 3或-1 | C. | 3或-3 | D. | 1或-1 |
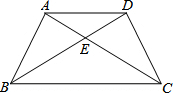 如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC. 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.