题目内容
在圆中,一条弧所对的圆心角和圆周角分别是(4x-60)°和(3x-70)°,求这条弧所对的圆心角和圆周角的度数.
考点:圆心角、弧、弦的关系,圆周角定理
专题:
分析:由在圆中,一条弧所对的圆心角和圆周角分别为(4x-60)°和(3x-70)°,根据圆周角定理,即可得4x-60=2(3x-70),解此方程即可求得答案.
解答:解:∵一条弧所对的圆心角和圆周角分别为(4x-60)°和(3x-70)°,
∴4x-60=2(3x-70),
解得:x=40,
故这条弧所对的圆心角和圆周角的度数分别是:100°,50°.
∴4x-60=2(3x-70),
解得:x=40,
故这条弧所对的圆心角和圆周角的度数分别是:100°,50°.
点评:此题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.此题难度不大,注意掌握方程思想的应用.同时考查了圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
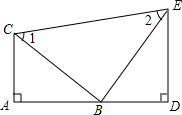 已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.
已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.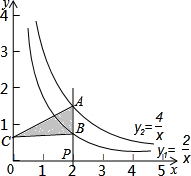 如图,过x轴正半轴任意一点P作x轴的垂线,分别与反比例函数y1=
如图,过x轴正半轴任意一点P作x轴的垂线,分别与反比例函数y1=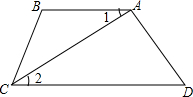 根据下列证明过程填空:如图,已知AB∥CD,∠B=120°,CA平分∠BCD,求证:∠1=30°
根据下列证明过程填空:如图,已知AB∥CD,∠B=120°,CA平分∠BCD,求证:∠1=30°