题目内容
5．如果|5-a|+（b+3）2=0，那么代数式$\frac{1}{a}$（1-2b）的值为$\frac{7}{5}$．分析 根据绝对值和偶次方的非负性求出a、b的值，再代入求出即可．
解答 解：∵|5-a|+（b+3）2=0，
∴5-a=0，b+3=0，
∴a=5，b=-3，
∴$\frac{1}{a}$（1-2b）=$\frac{1}{5}$×[1-2×（-3）]=$\frac{7}{5}$，
故答案为：$\frac{7}{5}$．
点评 本题考查了绝对值、偶次方的非负性和求代数式的值等知识点，能求出a、b的值是解此题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18．以下说法正确的是（ ）
| A． | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4，则xy的平方根为1 | B． | 3-2$\sqrt{2}$的绝对值是2$\sqrt{2}$-3 | ||
| C． | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立，则a≤0且b≥0 | D． | 若$\sqrt{（1-a）^{2}}$+$\sqrt{（a-3）^{2}}$=2，则a≥3 |
13．函数y=$\frac{k}{x}$的图象经过点（-4，6），则下列各点中在y=$\frac{k}{x}$图象上的是（ ）
| A． | （3，8） | B． | （3，-8） | C． | （-8，-3） | D． | （-4，-6） |
10．
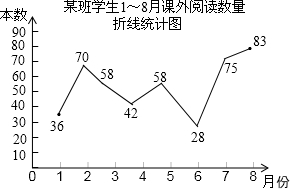班长统计了今年1～8月“书香校园”活动中全班同学的课外阅读数量是（单位：本），绘制了如图折线统计图，下列说法正确的是（ ）
班长统计了今年1～8月“书香校园”活动中全班同学的课外阅读数量是（单位：本），绘制了如图折线统计图，下列说法正确的是（ ）| A． | 平均数是45 | B． | 众数是42 | C． | 中位数是58 | D． | 方差小于10 |