题目内容
14.若关于y的一元二次方程ky2-4y-3=3y+4有实根,求k的取值范围.分析 首先把方程化为一般形式ax2+bx+c=0,再根据方程有实根可得△=b2-4ac≥0,再代入a、b、c的值再解不等式即可.
解答 解:ky2-4y-3=3y+4,
移项得:ky2-4y-3-3y-4=0,
合并同类项得:ky2-7y-7=0,
∵方程有实数根,
∴△≥0且k≠0,
(-7)2-4k×(-7)=49+28k≥0,
解得:k≥-$\frac{7}{4}$.
∴k的取值范围为:k≥-$\frac{7}{4}$且k≠0.
点评 此题主要考查了根的判别式,关键是掌握一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.三角形的外心具有的性质是( )
| A. | 到三个顶点的距离相等 | B. | 到三边的距离相等 | ||
| C. | 是三角形三条角平分线的交点 | D. | 是三角形三条中线的交点 |
3. 表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
 表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | a×b>0 | D. | |a|>b |
 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,垂足为E,AD平分∠BAC.
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,垂足为E,AD平分∠BAC.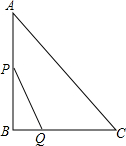 如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.
如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.