Question

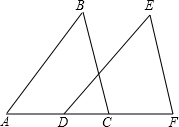如图，点D，C在AF上，AB=DE，AD=CF，BC=EF，求证：DE∥AB．

Answer 1

考点：全等三角形的判定与性质

专题：证明题

分析：求出AC=DF，再利用“边边边”证明△ABC和△DEF全等，根据全等三角形对应角相等可得∠A=∠EDF，然后根据同位角相等，两直线平行证明即可．

解答：证明：∵AD=CF，
∴AD+CD=CF+CD，
即AC=DF，
在△ABC和△DEF中，

AB=DE AC=DF BC=EF

，
∴△ABC≌△DEF（SSS），
∴∠A=∠EDF，
∴DE∥AB．

点评：本题考查了全等三角形的判定与性质，平行线的判定，熟练掌握三角形全等的判定方法是解题的关键，易错点在于需要先求出AC=DF．