题目内容
我们把从1开始的几个连续自然数的立方和记为Sn,那么有:
S1=13=12=[
]2
S2=13+23=(1+2)2=[
]2
S3=13+23+33=(1+2+3)2=[
]2
S4=13+23+33+43=(1+2+3+4)2=[
]2
…
观察上面的规律,完成下面各题:
(1)写出S5,S6的表达式;
(2)探索写出Sn的表达式;
(3)求113+123+…+203的值.
S1=13=12=[
| 1×(1+1) |
| 2 |
S2=13+23=(1+2)2=[
| 2×(1+2) |
| 2 |
S3=13+23+33=(1+2+3)2=[
| 3×(1+3) |
| 2 |
S4=13+23+33+43=(1+2+3+4)2=[
| 4×(1+4) |
| 2 |
…
观察上面的规律,完成下面各题:
(1)写出S5,S6的表达式;
(2)探索写出Sn的表达式;
(3)求113+123+…+203的值.
考点:有理数的乘方
专题:规律型
分析:(1)本题需先根据S1、S2、S3所给的规律,分别是1、2、3、的三次方进行相加,由此可以得出S5和S6的答案.
(2)本题需先根据(1)的规律即可得出Sn的表示方法即可.
(3)本题需先根据Sn的公式,再结合原式=S20-S10,即可求出正确答案.
(2)本题需先根据(1)的规律即可得出Sn的表示方法即可.
(3)本题需先根据Sn的公式,再结合原式=S20-S10,即可求出正确答案.
解答:解:(1)S5=13+23+33+43+53=(1+2+3+4+5)2=【
】2,
S6=13+23+33+43+53+63=(1+2+3+4+5+6)2=【
】2;
(2)Sn=[
]2
(3)原式=S20-S10=【
】2-【
】2=41075.
| 5×(1+5) |
| 2 |
S6=13+23+33+43+53+63=(1+2+3+4+5+6)2=【
| 6×(1+6) |
| 2 |
(2)Sn=[
| n(1+n) |
| 2 |
(3)原式=S20-S10=【
| 20×(1+20) |
| 2 |
| 10×(1+10) |
| 2 |
点评:本题主要考查了数字的变化类,在解题时要根据已知条件找出题中的规律是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,BD、CE为△ABC的两条内角平分线,K为ED的中点,KF⊥AB于F,KG⊥AC于G,KH⊥BC于H,求证:KF+KG=KH.
如图,BD、CE为△ABC的两条内角平分线,K为ED的中点,KF⊥AB于F,KG⊥AC于G,KH⊥BC于H,求证:KF+KG=KH. 如图,在平行四边形OABC中,OA=8,AB=6,∠AOC=120°,求点A,O,C,B各点的坐标.
如图,在平行四边形OABC中,OA=8,AB=6,∠AOC=120°,求点A,O,C,B各点的坐标.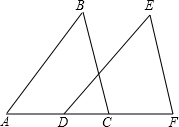 如图,点D,C在AF上,AB=DE,AD=CF,BC=EF,求证:DE∥AB.
如图,点D,C在AF上,AB=DE,AD=CF,BC=EF,求证:DE∥AB.