题目内容
17.计算$\sqrt{50}$-$\sqrt{18}$的结果为2$\sqrt{2}$.分析 首先把代数式中的二次根式进行化简,再合并同类二次根式即可.
解答 解:原式=5$\sqrt{2}$-3$\sqrt{2}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 此题主要考查了二次根式的减法,关键是掌握计算法则:二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.

练习册系列答案
相关题目
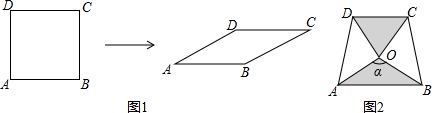
7.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
(2)填空:
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).

(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
12.下列x的值能使$\sqrt{x-4}$有意义的是( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=5 |
2.八年级的同学们即将步入初三,某主题班会小组为了了解本校八年级同学对初三的第一印象,打算抽样调查40位同学.
(1)有同学提议:“八年级1班的人数刚好是40人,不如我们直接调查1班所有同学吧”,他的建议合理吗?请说明理由;
(2)他们用问卷随机调查了40位同学(每人只能选一项),并统计如下:
请选择一种统计图将上表中的数据描述出来;
(3)若本校八年级共有500名学生,请估计对初三第一印象是“忧喜交加”的同学人数.
(1)有同学提议:“八年级1班的人数刚好是40人,不如我们直接调查1班所有同学吧”,他的建议合理吗?请说明理由;
(2)他们用问卷随机调查了40位同学(每人只能选一项),并统计如下:
| 第一印象 | 满怀期待 | 忧喜交加 | 想想都累 | 放过我吧 | 其他 |
| 划记 | 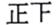 | 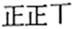 |  | 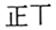 |  |
(3)若本校八年级共有500名学生,请估计对初三第一印象是“忧喜交加”的同学人数.

