题目内容
13.已知:矩形ABCD中,AB=1,AD=a,在BC边上存在唯一一点Q,使AQ⊥DQ,求a.分析 以AD为直径作圆,结合在BC边上存在唯一一点Q使AQ⊥DQ,即可得出点Q为线段BC的中点,根据勾股定理即可得出关于a的方程,解方程即可得出a的值.
解答 解:以AD为直径作圆,如图所示.
∵在BC边上存在唯一一点Q,使AQ⊥DQ,
∴点Q为线段BC的中点.
在Rt△ABQ中,AB=1,BQ=$\frac{1}{2}$BC=$\frac{1}{2}$a,
∴AQ=$\sqrt{A{B}^{2}+B{Q}^{2}}$=$\sqrt{1+\frac{{a}^{2}}{4}}$,
同理可得:DQ=AQ=$\sqrt{1+\frac{{a}^{2}}{4}}$.
在Rt△ADQ中,AQ=DQ=$\sqrt{1+\frac{{a}^{2}}{4}}$,
∴AD=$\sqrt{2}$AQ=$\sqrt{2}$$\sqrt{1+\frac{{a}^{2}}{4}}$=a,
解得:a=2.或a=-2(舍去).
点评 本题考查了矩形的性质以及勾股定理,解题的关键是找出点Q的位置.本题属于基础题,难度不大,解决该题型题目时,借助于画圆找出点Q的位置是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3.下列几组数中,为勾股数的是( )
| A. | 3、4、6 | B. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | C. | 7、24、25 | D. | 0.9、1.2、1.6 |
4. 如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为( )
如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为( )
 如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为( )
如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
1.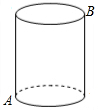 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 6 cm | B. | 8 cm | C. | 10 cm | D. | 12 cm |



 ,-2,-
,-2,- 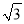 的大小,其中最小的实数是( ).
的大小,其中最小的实数是( ). C. -2 D. -
C. -2 D. -