题目内容
18.当0<x<1时,化简$\sqrt{\frac{x^2+4}{2x}+2}$+$\sqrt{\frac{x^2+4}{2x}-2}$.分析 根据二次根式的性质化简,即可解答.
解答 解:当0<x<1时,
$\sqrt{\frac{x^2+4}{2x}+2}$+$\sqrt{\frac{x^2+4}{2x}-2}$
=$\sqrt{\frac{{x}^{2}+4+4x}{2x}}+\sqrt{\frac{{x}^{2}+4-4x}{2x}}$
=$\sqrt{\frac{(x+2)^{2}}{2x}}+\sqrt{\frac{(x-2)^{2}}{2x}}$
=$\frac{(x+2)\sqrt{2x}}{2x}+\frac{-(x-2)\sqrt{2x}}{2x}$
=$\frac{(x+2-x+2)\sqrt{2x}}{2x}$
=$\frac{2\sqrt{2x}}{x}$.
点评 本题考查了二次根式的性质与化简,解决本题的关键是根据二次根式的性质化简.

练习册系列答案
相关题目
7.图象过点P(3,4)的正比例函数是( )
| A. | y=$\frac{3}{4}$x | B. | y=$\frac{12}{x}$ | C. | y=x+1 | D. | y=$\frac{4}{3}$x |
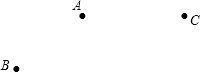 已知平面上三点A、B、C.按下列要求画出图形:
已知平面上三点A、B、C.按下列要求画出图形:
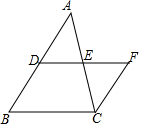 如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF.
如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF.