题目内容
7.图象过点P(3,4)的正比例函数是( )| A. | y=$\frac{3}{4}$x | B. | y=$\frac{12}{x}$ | C. | y=x+1 | D. | y=$\frac{4}{3}$x |
分析 设正比例函数为y=kx,(k≠0),把点P的坐标代入函数解析式,求得k的值即可.
解答 解:设正比例函数为y=kx,(k≠0),
∵正比例函数y=kx的图象过点P(3,4),
4=3k,
解得,k=$\frac{4}{3}$,
∴该函数关系式为:y=$\frac{4}{3}$x;
故选D.
点评 本题考查了待定系数法求正比例函数解析式,设出函数解析式,然后将点的坐标代入解析式,利用方程解决问题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
2.在南水北调正是通水之前,某学校在征得上级教育主管部分的批准后,计划组织本校七八年级学生自愿参加某旅行社的“渠首一日游”活动,此项活动的收费标准如下:
已知该校七年级报名参加的学生人数多于100人,八年级报名参加的学生人数少于100人,经核算,若七八年级分别组团共需花费20800元,若七八年级联合组团只需花费18000元.
(1)七八年级报名参加旅游的学生人数之和超过200人么?为什么?
(2)七八年级报名参加旅游的学生各有多少人?
| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 85 | 75 |
(1)七八年级报名参加旅游的学生人数之和超过200人么?为什么?
(2)七八年级报名参加旅游的学生各有多少人?
16.已知三角形的两边之长分别为3cm和5cm,则第三边的长可能为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 10cm |
17.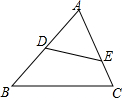 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )| A. | ∠B=∠AED | B. | AE•AC=AD•AB | C. | ∠C=∠ADE | D. | $\frac{AE}{AB}=\frac{DE}{BC}$ |
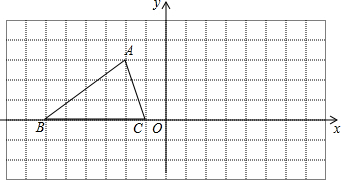 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0). 如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.
如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.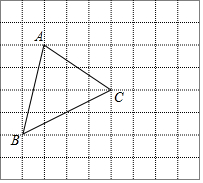 如图,△ABC的有三个顶点都在边长为1的小正方形网格的格点上.
如图,△ABC的有三个顶点都在边长为1的小正方形网格的格点上.