题目内容
8.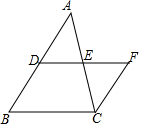 如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF.
如图,△ABC中,D是AB的中点,CF∥AB,DF交AC于点E,DE=EF.(1)求证:四边形DBCF是平行四边形;
(2)若BC=AC=10,CF=6,求四边形DBCF的面积.
分析 (1)由条件可证明△ADE≌△CFE,可证得CF=AD,则可证得四边形DBCF是平行四边形;
(2)连接CD可知CD⊥AB,由勾股定理可求得CD的长,则可求得答案.
解答 (1)证明:
∵CF∥AB,
∴∠A=∠ECF,
在△ADE和△CFE中
$\left\{\begin{array}{l}{∠A=∠ECF}\\{∠AED=∠CEF}\\{DE=EF}\end{array}\right.$,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵D是AB的中点,
∴AD=BD,
∴BD=CF,且BD∥CF,
∴四边形DBCF是平行四边形;
(2)解:
连接CD,如图,
∵CA=CB,D为AB中点,
∴CD⊥AB,
∵四边形DBCF是平行四边形,
∴BD=CF=6,且BC=10,
在Rt△BCD中,可求得CD=8,
∴S四边形DBCF=BD•CD=6×8=48.
点评 本题主要考查平行四边形的判定和性质,在(1)中求得AD=CF是解题的关键,在(2)中证得CD是四边形DBCF的高是解题的关键.

练习册系列答案
相关题目
16.已知三角形的两边之长分别为3cm和5cm,则第三边的长可能为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 10cm |
17.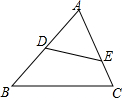 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
 如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )
如图,D、E分别为△ABC中AB、AC边上的点,添加一个条件,使△ADE与△ABC相似,添加的条件错误是( )| A. | ∠B=∠AED | B. | AE•AC=AD•AB | C. | ∠C=∠ADE | D. | $\frac{AE}{AB}=\frac{DE}{BC}$ |
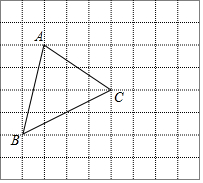 如图,△ABC的有三个顶点都在边长为1的小正方形网格的格点上.
如图,△ABC的有三个顶点都在边长为1的小正方形网格的格点上.