题目内容
6.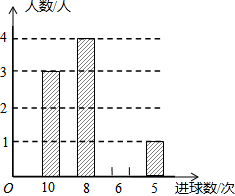 某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.| 次数 | 10 | 8 | 6 | 5 |
| 人数 | 3 | a | 2 | 1 |
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?
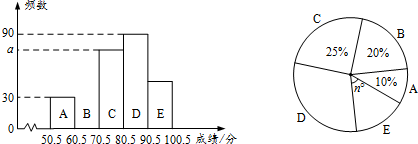
分析 (1)根据条形统计图可知a=4;
(2)根据表格数据可知6次的人数是2,然后补全统计图即可;
(3)根据小组成员共10人,投进10球的成员有3人,再概率公式进行求解即可.
解答 解:(1)由条形统计图可知次数为8的有4人,
则a=4;
故答案为:4;
(2)由表可知,6次的有2人,
补全统计图如图;
(3)∵小组成员共10人,投进10球的成员有3人,
∴P=$\frac{3}{10}$,
答:从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率是$\frac{3}{10}$.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.已知点P1(-4,3)和P2(-4,-3),则P1和P2( )
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 不存在对称关系 |
17.某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( )
| A. | $\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=2 | B. | $\frac{1200}{(1-20%)x}$-$\frac{1200}{x}$=2 | ||
| C. | $\frac{1200}{(1+20%)x}$-$\frac{1200}{x}$=2 | D. | $\frac{1200}{x}$-$\frac{1200}{(1-20%)x}$=2 |
14.如果把分式$\frac{xy}{x+y}$中的x和y都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的4倍 | B. | 扩大为原来的2倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{2}$ |
11.一组数据2,0,-2,1,3的中位数是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 1.5 |
3.下列语句中正确的是( )
| A. | 在所有连结两点的线中,直线最短 | |
| B. | ∠AOB与∠BOA表示相同的角 | |
| C. | 一个锐角与一个钝角的和是一个平角 | |
| D. | 两点之间的线段是两点之间的距离 |