题目内容
14.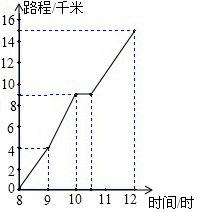 如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:(1)在这个变化过程中,自变量是时间,因变量是路程.
(2)9时所走的路程是多少?他休息了多长时间?
(3)他从休息后直至到达目的地这段时间的平均速度是多少?
分析 (1)根据数量关系路程=速度×时间,结合函数图象即可得出:自变量为时间,因变量为路程;
(2)找出当时间为9时时的路程,再找出休息的起始时间即可得出结论;
(3)利用速度=路程÷时间即可求出结论.
解答 解:(1)∵数量关系:路程=速度×时间,
∴结合图形即可得出:自变量为时间,因变量为路程.
故答案为:时间;路程.
(2)∵当时间为9时时,路程为4千米,
∴9时所走的路程是4千米.
10.5-10=0.5小时=30分钟.
∴他休息了30分钟.
(3)(15-9)÷(12-10.5)=4(千米/时).
答:他从休息后直至到达目的地这段时间的平均速度是4千米/时.
点评 本题考查了函数的图象以及常量与变量,解题的关键是:(1)根据图象找出自变量及因变量;(2)了解坐标系中点表示的意义;(3)根据数量关系列式计算.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).
如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).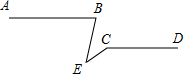 如图,AB∥CD,请探索∠B,∠C,∠E的关系?
如图,AB∥CD,请探索∠B,∠C,∠E的关系?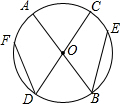 如图,AB,CD是⊙O的直径,DF,BE是弦,且DF=BE,求证:$\widehat{AF}$=$\widehat{CE}$.
如图,AB,CD是⊙O的直径,DF,BE是弦,且DF=BE,求证:$\widehat{AF}$=$\widehat{CE}$.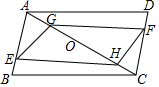 如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形.
如图,已知在平行四边形ABCD中,BE=DF,AG=CH,求证:四边形GEHF是平行四边形.