题目内容
 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )A、5,
| ||
B、7,90°+
| ||
C、10,90°-
| ||
D、10,90°+
|
考点:切线长定理
专题:
分析:根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;连接OA、OE、OB根据切线性质,∠P+∠AOB=180°,再根据CD为切线可知∠COD=
∠AOB.
| 1 |
| 2 |
解答: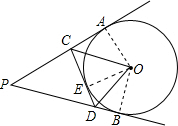 解:∵PA、PB切⊙O于A、B,CD切⊙O于E,
解:∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,;
如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
∠AOB,
∴∠AOB=180°-∠P,
∴∠COD=90°-
∠P.
故选:C.
 解:∵PA、PB切⊙O于A、B,CD切⊙O于E,
解:∵PA、PB切⊙O于A、B,CD切⊙O于E,∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,;
如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
| 1 |
| 2 |
∴∠AOB=180°-∠P,
∴∠COD=90°-
| 1 |
| 2 |
故选:C.
点评:本题考查了切线的性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题,是基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某商店卖出两件衣服,每件60元,其中一件赚20%,另一件亏20%,那么这两件衣服卖出后,商店( )
| A、不赚不亏 | B、赚5元 |
| C、亏5元 | D、赚10元 |
下列关于x的函数中,一定是二次函数的是( )
| A、y=ax2+bx+c | ||
B、y=x2+
| ||
| C、y=2x+c2 | ||
| D、y=(x-k)2+h |
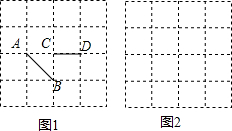 如图,正方形网格中的每个小正方形边长都是1.
如图,正方形网格中的每个小正方形边长都是1.