题目内容
 如图,已知在△ABC中,AB=AC,BC比AB大3,sinB=
如图,已知在△ABC中,AB=AC,BC比AB大3,sinB=| 4 |
| 5 |
(1)求AG的长;
(2)当∠APQ=90°时,直线PG与边BC相交于点M.求
| AQ |
| MQ |
(3)当点Q在边AC上时,设BP=x,AQ=y,求y关于x的函数解析式,并写出它的定义域.
考点:相似形综合题
专题:
分析:(1)根据已知条件和重心的性质得出BD=DC=
BC,AD⊥BC,再根据sinB=
=
,求出AB、BC、AD的值,从而求出AG的长;
(2)根据∠GMD+∠MGD=90°和∠GMD+∠B=90°,得出∠MGD=∠B,再根据特殊角的三角函数值求出DM、CM=CD-DM的值,在△ABC中,根据AA求出△QCM∽△QGA,即可求出
的值;
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF,得出
=
,求出BE的值,同理可得出CF的值,最后根据BD=CD,求出EG=FG,即可得出CE+BE=2GD,从而得出求y关于x的函数解析式并得出它的定义域.
| 1 |
| 2 |
| AD |
| AB |
| 4 |
| 5 |
(2)根据∠GMD+∠MGD=90°和∠GMD+∠B=90°,得出∠MGD=∠B,再根据特殊角的三角函数值求出DM、CM=CD-DM的值,在△ABC中,根据AA求出△QCM∽△QGA,即可求出
| AQ |
| MQ |
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF,得出
| AP |
| BP |
| AG |
| BE |
解答:解:(1)在△ABC中,
∵AB=AC,点G是△ABC的重心,
∴BD=DC=
BC,
∴AD⊥BC.
在Rt△ADB中,
∵sinB=
=
,
∴
=
.
∵BC-AB=3,
∴AB=15,BC=18.
∴AD=12.
∵G是△ABC的重心,
∴AG=
AD=8.
(2)在Rt△MDG,
∵∠GMD+∠MGD=90°,
同理:在Rt△MPB中,∠GMD+∠B=90°,
∴∠MGD=∠B.
∴sin∠MGD=sinB=
,
在Rt△MDG中,∵DG=
AD=4,
∴DM=
,
∴CM=CD-DM=
,
在△ABC中,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
∵∠QCM=∠CDA+∠DAC=90°+∠DAC,
又∵∠QGA=∠APQ+∠BAD=90°+∠BAD,
∴∠QCM=∠QGA,
又∵∠CQM=∠GQA,
∴△QCM∽△QGA.
∴
=
=
.
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF.
∵BE∥AD,∴
=
,即
=
,
∴BE=
.
同理可得:
=
,即
=
,
∴CF=
.
∵BE∥AD∥CF,BD=CD,
∴EG=FG.
∴CF+BE=2GD,即
+
=8,
∴y=
,(0≤x≤
).
∵AB=AC,点G是△ABC的重心,
∴BD=DC=
| 1 |
| 2 |
∴AD⊥BC.
在Rt△ADB中,
∵sinB=
| AD |
| AB |
| 4 |
| 5 |
∴
| BD |
| AB |
| 3 |
| 5 |
∵BC-AB=3,
∴AB=15,BC=18.
∴AD=12.
∵G是△ABC的重心,
∴AG=
| 2 |
| 3 |
(2)在Rt△MDG,
∵∠GMD+∠MGD=90°,
同理:在Rt△MPB中,∠GMD+∠B=90°,
∴∠MGD=∠B.
∴sin∠MGD=sinB=
| 4 |
| 5 |

在Rt△MDG中,∵DG=
| 1 |
| 3 |
∴DM=
| 16 |
| 3 |
∴CM=CD-DM=
| 11 |
| 3 |
在△ABC中,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
∵∠QCM=∠CDA+∠DAC=90°+∠DAC,
又∵∠QGA=∠APQ+∠BAD=90°+∠BAD,
∴∠QCM=∠QGA,
又∵∠CQM=∠GQA,
∴△QCM∽△QGA.
∴
| AQ |
| MQ |
| AG |
| MC |
| 24 |
| 11 |
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF.
∵BE∥AD,∴
| AP |
| BP |
| AG |
| BE |
| 15-x |
| x |
| 8 |
| BE |
∴BE=
| 8x |
| 15-x |
同理可得:
| AQ |
| QC |
| AG |
| CF |
| y |
| 15-y |
| 8 |
| CF |

∴CF=
| 8(15-y) |
| y |
∵BE∥AD∥CF,BD=CD,
∴EG=FG.
∴CF+BE=2GD,即
| 8(15-y) |
| y |
| 8x |
| 15-x |
∴y=
| 75-5x |
| 10-x |
| 15 |
| 2 |
点评:此题考查了相似形的综合,用到的知识点是重心、特殊角的三角函数值、相似三角形的判定与性质、平行线的性质等,关键是根据题意,画出图形,做出辅助线,构造直角三角形是本题的关键.

练习册系列答案
相关题目
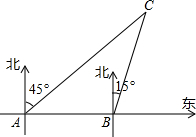 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C. 已知△ABC,求作内切圆(保留作图痕迹,不写作法)
已知△ABC,求作内切圆(保留作图痕迹,不写作法)