题目内容
3.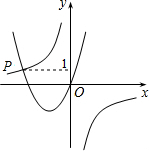 如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.
如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.
分析 根据函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,可以求得点P的坐标,再将两个函数联立方程组即可变形为题目中的方程,从而可以得到问题的答案.
解答 解:∵函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,
∴将y=-1代入函数y=$\frac{-3}{x}$,得x=-3,
∴点P的坐标为(-3,1),
∵$\left\{\begin{array}{l}{y=\frac{-3}{x}}\\{y=a{x}^{2}+bx+c}\end{array}\right.$
∴$a{x}^{2}+bx+c=\frac{-3}{x}$
又∵有函数图象可知y=ax2+bx+c过点(0,0),
∴c=0,
∴$a{x}^{2}+bx=\frac{-3}{x}$
即$a{x}^{2}+bx+\frac{3}{x}=0$
∵函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,
∴方程$a{x}^{2}+bx+\frac{3}{x}=0$的解是:x=-3,y=1,
故答案为:x=-3,y=1.
点评 本题考查二次函数的图象、反比例函数的图象,解题的关键是利用数形结合的思想,将它们联系起来,然后找出所求问题需要的条件.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
14.在Rt△ABC中,∠C=90°,AB=5,AC=3.下列选项中,正确的是( )
| A. | sinA=$\frac{3}{5}$ | B. | cosA=$\frac{3}{5}$ | C. | tanA=$\frac{3}{5}$ | D. | cotA=$\frac{3}{5}$ |
18.按下面的程序计算:

若输入x=100,则输出结果是501;若输入x=25,则输出结果是631;若开始输入的数x为正整数,最后输出结果为781,则开始输入的数x的所有可能的值为1或6或31或156.

若输入x=100,则输出结果是501;若输入x=25,则输出结果是631;若开始输入的数x为正整数,最后输出结果为781,则开始输入的数x的所有可能的值为1或6或31或156.
8.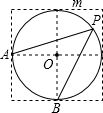 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )
 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )| A. | 45° | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 无法确定 |
11.已知一组数据:16,15,16,14,17,16,15,则众数是( )
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
