题目内容
11.如图,∠MAN=45°,点C在射线AM上,AC=10,过C点作CB⊥AN交AN 于点B,P为线段AC上一个动点,Q点为线段AB上的动点,且始终保持PQ=PB.
(1)如图1,若∠BPQ=45°,求证:△ABP是等腰三角形;
(2)如图2,DQ⊥AP于点D,试问:此时PD的长度是否变化?若变化,请说明理由;若不变,请计算其长度;
(3)当点P运动到AC的中点时,将△PBQ以每秒1个单位的速度向右匀速平移,设运动时间为t秒,B点平移后的对应点为E,求△ABC和△PQE的重叠部分的面积.
分析 (1)由PQ=PB,求得∠PBQ=∠PQB=67.5°,∠APB=180°-45°-67.5°=67.5°,即可得出△ABP为等腰三角形;
(2)PD的长度不变化,过点B作BH⊥AC于点H,由AAS证得△PDQ≌△PBH,得出PD=BH=$\frac{1}{2}$AC=5;
(3)当点P运动到AC的中点时,则点Q与点A重合,△BPQ为等腰直角三角形,QP=PB=$\frac{1}{2}$AC=5,AB=5$\sqrt{2}$,将△PBQ向右平移,点P落到BC上时,平移了$\frac{5\sqrt{2}}{2}$个单位,点Q与点B重合时,平移了5$\sqrt{2}$个单位,分三种情况讨论,①当0<t<$\frac{{5\sqrt{2}}}{2}$时,S=S△PQE-S△BEF=$\frac{25}{2}-\frac{1}{2}{t^2}$;②当$\frac{{5\sqrt{2}}}{2}$≤t<$5\sqrt{2}$时,$S=\frac{1}{2}B{Q^2}=\frac{1}{2}×{({5\sqrt{2}-t})^2}$=${t^2}-5\sqrt{2}t+25$;③当t≥$5\sqrt{2}$时,s=0.
解答 (1)证明:∵∠BPQ=45°,PQ=PB,
∴∠PBQ=∠PQB=67.5°,
∵∠MAN=45°,
∴∠APB=180°-45°-67.5°=67.5°,
∴∠APB=∠PBQ,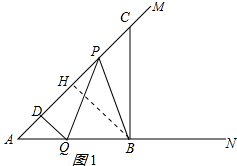
∴△ABP为等腰三角形;
(2)解:PD的长度不变化,
过点B作BH⊥AC于点H,如图1所示:
∵DQ⊥AP,
∴∠PDQ=∠PHB=90°,
∵∠MAN=45°,
∴∠HBA=45°,
∴∠DPQ=∠PQB-∠MAN=∠PBQ-∠HBA=∠PBH,
在△PDQ和△PBH中,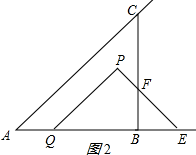 $\left\{\begin{array}{l}{∠DPQ=∠PBH}\\{∠PDQ=∠BHP=90°}\\{PQ=PB}\end{array}\right.$,
$\left\{\begin{array}{l}{∠DPQ=∠PBH}\\{∠PDQ=∠BHP=90°}\\{PQ=PB}\end{array}\right.$,
∴△PDQ≌△PBH(AAS),
∴PD=BH=$\frac{1}{2}$AC=5;
(3)解:当点P运动到AC的中点时,
则点Q与点A重合,∠QPB=90°,∠PQB=∠PBQ=45°,QP=PB=$\frac{1}{2}$AC=5,AB=5$\sqrt{2}$,
将△PBQ向右平移,点P落到BC上时,平移了$\frac{5\sqrt{2}}{2}$个单位,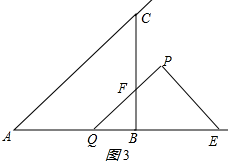 点Q与点B重合时,平移了5$\sqrt{2}$个单位,分三种情况讨论,
点Q与点B重合时,平移了5$\sqrt{2}$个单位,分三种情况讨论,
①当0<t<$\frac{{5\sqrt{2}}}{2}$时,如图2所示:
S=S△PQE-S△BEF=$\frac{25}{2}-\frac{1}{2}{t^2}$;
②当$\frac{{5\sqrt{2}}}{2}$≤t<$5\sqrt{2}$时,如图3所示:
$S=\frac{1}{2}B{Q^2}=\frac{1}{2}×{({5\sqrt{2}-t})^2}$=${t^2}-5\sqrt{2}t+25$;
③当t≥$5\sqrt{2}$时,△PQE移出了△ABC,s=0.
综上所述:△ABC和△PQE的重叠部分的面积为$\frac{25}{2}-\frac{1}{2}{t^2}$(0<t<$\frac{{5\sqrt{2}}}{2}$),或${t^2}-5\sqrt{2}t+25$($\frac{{5\sqrt{2}}}{2}$≤t<$5\sqrt{2}$),或0(t≥$5\sqrt{2}$).
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、平移的性质、等腰直角三角形的性质、三角形面积的计算等知识;本题综合性强,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | x6÷x3=x8 | B. | x3+x2=x6 | C. | (x2)3=x5 | D. | x2•x3=x5 |
| A. | 1.11×104 | B. | 11.1×104 | C. | 1.11×105 | D. | 1.11×106 |
| A. | 第二、四象限 | B. | 第一、二、三象限 | C. | 第一、三象限 | D. | 第二、三、四象限 |
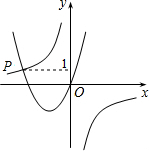 如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.
如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.