题目内容
8.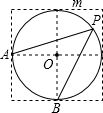 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧$\widehat{AmB}$上的一点,则cos∠APB的值是( )| A. | 45° | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 无法确定 |
分析 根据题意求出∠AOB=90°,根据圆周角定理求出∠APB的度数,运用特殊角的三角函数值计算即可.
解答 解:由题意和正方形的性质得,∠AOB=90°,
∴∠APB=$\frac{1}{2}$∠AOB=45°,
∴cos∠APB=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查的是圆周角定理和特殊角的三角函数值,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、熟记特殊角的三角函数值是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.-2的绝对值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | -|2| |
20.一条直线y=kx+b,其中k+b<0,kb>0,那么该直线经过( )
| A. | 第二、四象限 | B. | 第一、二、三象限 | C. | 第一、三象限 | D. | 第二、三、四象限 |
17.李明为了了解本班同学的身高情况,随机抽取了一部分同学进行身高测量,获得如下数据(单位:cm):139,118,137,129,135,156,148,137,112,149,139,135,138,117,116,160.
(1)根据以上数据填表:
(2)以上这种调查方式称为抽样调查(填“全面”或“抽样”);
(3)要直观地反映各身高段人数的多少,应画条形统计图比较合适;要直观地反映各身高段人数占被调查人数的百分比,应画扇形统计图比较合适.
(1)根据以上数据填表:
| 身高h(单位:cm) | 画记 | 人数 | 占调查人数的百分比(%) |
| h≤120 | 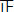 | 4 | 25% |
| 120<h≤140 | 正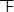 | 8 | 50% |
| h>140 | 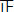 | 4 | 25% |
(3)要直观地反映各身高段人数的多少,应画条形统计图比较合适;要直观地反映各身高段人数占被调查人数的百分比,应画扇形统计图比较合适.
16.当x=2015时,分式$\frac{1-x}{{1-{x^2}}}$的值是( )
| A. | $\frac{1}{2015}$ | B. | $-\frac{1}{2015}$ | C. | $\frac{1}{2016}$ | D. | $-\frac{1}{2016}$ |
 ,则sinA=__.
,则sinA=__.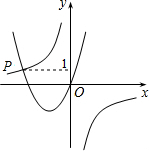 如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.
如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.