题目内容
14.在Rt△ABC中,∠C=90°,AB=5,AC=3.下列选项中,正确的是( )| A. | sinA=$\frac{3}{5}$ | B. | cosA=$\frac{3}{5}$ | C. | tanA=$\frac{3}{5}$ | D. | cotA=$\frac{3}{5}$ |
分析 首先在直角△ABC中利用勾股定理求得BC的长,然后利用三角函数的定义进行判断.
解答  解:在直角△ABC中BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
解:在直角△ABC中BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
A、sinA=$\frac{BC}{AB}$=$\frac{4}{5}$,选项错误;
B、cosA=$\frac{AC}{AB}$=$\frac{3}{5}$,选项正确;
C、tanA=$\frac{BC}{AC}$=$\frac{4}{3}$,选项错误;
D、cotA=$\frac{AC}{BC}$=$\frac{3}{4}$,选项错误.
故选B.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列计算正确的是( )
| A. | x6÷x3=x8 | B. | x3+x2=x6 | C. | (x2)3=x5 | D. | x2•x3=x5 |
9.△ABC中,∠A=60°,∠C=70°,则∠B的度数是( )
| A. | 50° | B. | 60° | C. | 70° | D. | 90° |
6.第二次全国残疾人抽样调查结果显示,我国0~6岁精神残疾儿童约为11.1万人,1.1万人用科学记数法表示为( )
| A. | 1.11×104 | B. | 11.1×104 | C. | 1.11×105 | D. | 1.11×106 |
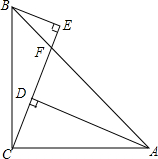 如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)
如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)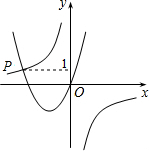 如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1.
如图,已知函数y=$\frac{-3}{x}$与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3,y=1. 有理数a,b在数轴上对应点的位置如图所示,化简|b-a|=a-b.
有理数a,b在数轴上对应点的位置如图所示,化简|b-a|=a-b.