题目内容
9. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出$\frac{BD}{CD}$=$\frac{BE}{AE}$,代入求出即可.
解答 解:∵根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF,
∵AF=4,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴$\frac{BD}{CD}$=$\frac{BE}{AE}$,
∵BD=6,AE=4,CD=3,
∴$\frac{6}{3}$=$\frac{BE}{4}$,
∴BE=8,
故选D.
点评 本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.

练习册系列答案
相关题目
20.三角形两边长分别为3和6,第三边的长是方程x2-13x+36=0的两根,则该三角形的周长为( )
| A. | 13 | B. | 15 | C. | 18 | D. | 13或18 |
14.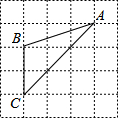 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
 某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米. 如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑) 如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)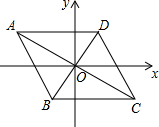 如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.