题目内容

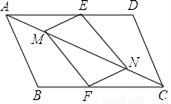
如图，在?ABCD中，点E，F分别在边AD，BC上，点M，N在对角线AC上，且AE=CF，AM=CN，求证：四边形EMFN是平行四边形．

证明见解析 【解析】试题分析：先由边角边证明△AEM≌△CFN ，得出EM=FN，EM∥FN即可解决问题． 试题解析：在平行四边形ABCD中，AD∥BC， ∴∠DAC=∠BCA， ∵AE=CF，AM=CN， ∴△AEM≌△CFN， ∴EM=FN，∠AME=∠CNF， ∴∠EMN=∠FNE， ∴EM∥FN， ∴四边形EMFN是平行四边形． ...
练习册系列答案
相关题目

已知△ABC的三边长为a、b、c，满足a+b=10，ab=18，c=8，则此三角形为_____三角形．

直角 【解析】根据已知：a+b=10，ab=18，c=8，可求（a+b）2﹣2ab=100﹣36=64，和c2=64，因此可得到a2+b2=c2，然后根据勾股定理可知此三角形是直角三角形． 故答案为：直角．

为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：

车型

目的地

A村（元/辆）

B村（元/辆）

大货车

800

900

小货车

400

600

（1）求这15辆车中大小货车各多少辆？

（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．

（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．

（1）大货车用8辆，小货车用7辆；（2）y=100x+9400．（3）见解析. 【解析】试题分析：（1）设大货车用x辆，小货车用y辆，根据大、小两种货车共15辆，运输152箱鱼苗，列方程组求解； （2）设前往A村的大货车为x辆，则前往B村的大货车为（8-x）辆，前往A村的小货车为（10-x）辆，前往B村的小货车为[7-（10-x）]辆，根据表格所给运费，求出y与x的函数关系式； ...

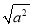我们这样来探究二次根式的结果，当a＞0时，如a=3，则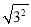=3，此时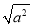的结果是a本身；当a=0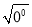时， =0．此时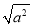的结果是零；当a＜0时，如a=﹣3，则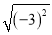=﹣（﹣3）=3，此时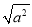的结果是a的相反数．这种分析问题的方法所体现的数学思想是（　　）

A. 分类讨论 B. 数形结合 C. 公理化 D. 转化

A 【解析】根据题意可知，探究过程是分三种情况讨论的，因此可知体现了数学思想是：分类讨论. 故选：A

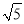如图，在矩形ABCD中，AB=4，BC=2，点E从点A出发，以每秒个单位长度的速度沿对角线AC向终点C运动，点F从点B出发，以每秒2个单位长度的速度沿边BA向终点A运动，连结EF，将线段EF绕点F顺时针旋转90°得到线段FG，以EF，FG为边作正方形EFGH，设点E运动的时间为t秒（t＞0）．

（1）用含t的代数式表示点E到边AB的距离．

（2）当点G落在边AB上时，求t的值．

（3）连结BG，设△BFG的面积为S平方单位（S＞0），求S与t之间的函数关系式．

（4）直接写出当正方形EFGH的顶点与点B，D距离相等时的t值．

（1）点E到边AB的距离为t（2）t=1（3）S= （4）当正方形EFGH的顶点与点B，D距离相等时的t值为s或1s或s 【解析】试题分析：（1）如图1中，作EM⊥AB于M．由EM∥BC，可得，即，延长即可解决问题； （2）如图2中，G在AB边时，由AF+FB=4，可得2t+2t=4，解方程即可； （3）分两种情形①如图3中，当0

如图，在小正方形的边长都为1的方格纸中，△ABO的顶点都在小正方形的顶点上，将△ABO绕点O顺时针方向旋转90°得到△A1B1O，则点A运动的路径长为_____．

【解析】在Rt△ABO中,OA===； 根据题意,知OA=OA1. 又∵∠AOA1=90°， ∴点A旋转至A1点所经过的轨迹长度==π. 故答案是： π.

如图，将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置，使点A，C，B′在同一条直线上，则旋转角的大小为（　　）

A. 45° B. 90° C. 120° D. 135°

D 【解析】∵△ABC为等腰直角三角形， ∴∠A=∠ACB=45°， ∴∠BCB′=180°?45°=135°， ∵等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置， ∴∠BCB′等于旋转角， 即旋转角为135°. 故选：D.

若x1=﹣1是关于x的方程x2+mx﹣5=0的一个根，则方程的另一个根x2=__．

5 【解析】试题分析：首先将x=－1代入方程求出m的值，然后再去解关于x的一元二次方程．

经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的，当三辆汽车经过这个十字路口时：

（1）请你用列表或画树状图的方法，表示出所有可能的结果；

（2）三辆车全部同向而行的概率是 ，至少有两辆车向左转的概率是 ；

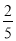（3）由于十字路口右拐弯处是通往新建经济开发区的，因此交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口向右转的频率为，向左转和直行的频率均为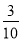．目前在此路口，汽车左转、右转、直行的绿灯亮的时间分别为30秒，在绿灯亮总时间不变的条件下，为了缓解交通拥挤，请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整．

（1）答案见解析；（2）； ；（3）答案见解析. 【解析】试题分析：（1）分别用A，B，C表示向左转、直行、向右转，根据题意，画出树形图；（2）从树状图中找出三辆车全部同向而行和至少有两辆车向左转的情况，计算出概率，其中至少有辆车向左包括两辆车向左和三辆车向左两种情况；（3）因为绿灯亮总时间不变，所以绿灯亮总时间仍为90（秒），再用90分别乘以左转、右转、直行的频率得到调整后的时间. ...

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网