题目内容
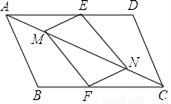
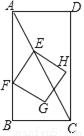
如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒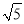 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
练习册系列答案
相关题目
在学校开展的“爱我中华”的一次演讲比赛中,编号1,2,3,4,5,6的五位同学最后成绩如表所示.那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 | 6 |
成绩/分 | 95 | 88 | 90 | 93 | 88 | 92 |
A. 92,88 B. 88,90 C. 88,92 D. 88,91
D 【解析】由表可知,这6为同学的成绩分别为:88、88、90、92、93、95, 则众数为88,中位数为(90+92) ÷2=91, 故选:D.

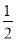 ,AB=3,求BD的长.
,AB=3,求BD的长.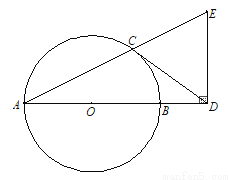
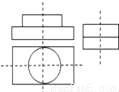
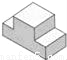 B.
B. 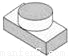 C.
C.  D.
D.