题目内容
20.已知一元二次方程x2-4x-3=0的两根为m,n,则m2+4n=19.分析 先利用一元二次方程的定义得到m2=4m+3,则m2+4n=4(m+n)+3,然后利用根与系数的关系进行计算即可.
解答 解:∵m为方程程x2-4x-3=0的根,
∴m2-4m-3=0,
∴m2=4m+3,
∴m2+4n=4m+3+4n=4(m+n)+3,
∵方程x2-4x-3=0的两根为m,n
∴m+n=4,
∴m2+4n=4×4+3=19.
故答案为19.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
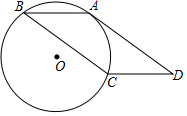 如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.



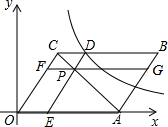 如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.
如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D. 如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.
如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.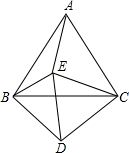 如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数是122°.
如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数是122°.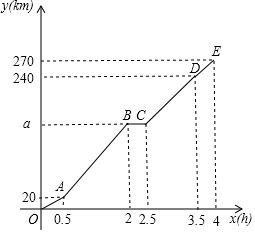 小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.
小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.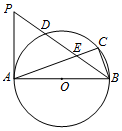 如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.