题目内容
已知点C在直线AB上,AB=6cm,BC=12cm,M是AC的中点,N是BC的中点,求MN的长.(用两种方式解答)
考点:两点间的距离
专题:
分析:根据题意画出图形,再根据各线段之间的关系进行解答.
解答: 解:如图1所示,
解:如图1所示,
∵AB=6cm,BC=12cm,
∴AC=AB+BC=6+12=18.
∵M是AC的中点,N是BC的中点,
∴CM=
AC=
×18=9,CN=
BC=
×12=6,
∴MN=CM-CN=9-6=3(cm);
如图2所示,
∵AB=6cm,BC=12cm,
∴AC=BC-AB=12-6=6.
∵M是AC的中点,N是BC的中点,
∴CM=
AC=
×6=3,点N与点A重合,
∴MN=AM=
AC=3(cm).
综上所述,MN的长为3cm.
 解:如图1所示,
解:如图1所示,∵AB=6cm,BC=12cm,
∴AC=AB+BC=6+12=18.
∵M是AC的中点,N是BC的中点,
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=CM-CN=9-6=3(cm);
如图2所示,
∵AB=6cm,BC=12cm,
∴AC=BC-AB=12-6=6.
∵M是AC的中点,N是BC的中点,
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=AM=
| 1 |
| 2 |
综上所述,MN的长为3cm.
点评:本题考查的是两点间的距离,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
三角形的外心是( )
| A、各内角的平分线的交点 |
| B、各边中线的交点 |
| C、各边垂线的交点 |
| D、各边垂直平分线的交点 |
 已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).
已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).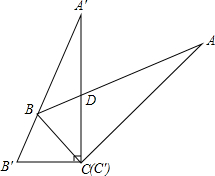 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C′的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数. 如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为
如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为 如图,在四边形ABCD中,∠A=45°,∠C=90°,∠ABD=75°,∠DBC=30°,AB=2a,求BC的长.
如图,在四边形ABCD中,∠A=45°,∠C=90°,∠ABD=75°,∠DBC=30°,AB=2a,求BC的长.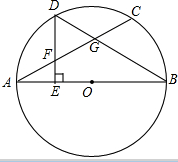 如图,AB是⊙O的直径,C是⊙O上一点,D是
如图,AB是⊙O的直径,C是⊙O上一点,D是